ও (পল্লগ (খ)) এ সমস্যার সমাধান করা যেতে পারে।
আমরা f(d, n)n এর চেয়ে কম বা সমান অঙ্কের সংখ্যার সাথে d দশমিক সংখ্যা পর্যন্ত পূর্ণসংখ্যার সংখ্যার হিসাবে সংজ্ঞায়িত করি । দেখা যায় যে এই ফাংশনটি সূত্র দ্বারা দেওয়া হয়েছে

আসুন সহজ কিছু দিয়ে শুরু করে এই ফাংশনটি উপস্থাপন করি।
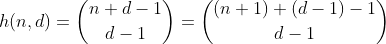
ফাংশন এইচটি এন + 1 বিভিন্ন উপাদান রয়েছে এমন একটি বহু সেট থেকে d - 1 টি উপাদান বেছে নেওয়ার উপায়গুলির সংখ্যা গণনা করে। এটি ডি বিনে বিভক্ত করার বিভিন্ন উপায়ের সংখ্যা, যা সহজেই ডি -1 বেড়া তৈরি করে এন এর চারপাশে সহজেই দেখা যায় এবং প্রতিটি পৃথক অংশকে সংযুক্ত করে। N = 2, d = 3 'এর উদাহরণ:
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
সুতরাং, এইচ সমস্ত সংখ্যার n এবং d সংখ্যার যোগফল গণনা করে। বাদে এটি কেবল 10 এর চেয়ে কম এন এর জন্য কাজ করে, যেহেতু অঙ্কগুলি 0 - 9 এর মধ্যে সীমাবদ্ধ। 10 - 19 মানের মানগুলির জন্য এটি ঠিক করতে, আমাদের 9 টিরও বেশি সংখ্যক একটি বিনের সাথে থাকা পার্টিশনের সংখ্যা বিয়োগ করতে হবে, আমি এখন থেকে ওভারফ্লাউন বিনগুলি কল করব।
নিম্নলিখিত পদটিতে h পুনরায় ব্যবহার করে এই শব্দটি গণনা করা যেতে পারে। আমরা n - 10 বিভাজন করার কয়েকটি উপায় গণনা করি, এবং তারপরে 10 টি স্থাপনের জন্য একটি বিন নির্বাচন করি, যার ফলশ্রুতিতে একটি ওভারফ্লাউন বিনের পার্টিশনের সংখ্যা রয়েছে। ফলাফলটি নিম্নলিখিত প্রাথমিক ক্রিয়াকলাপ।
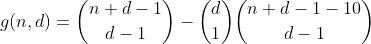
আমরা n-20 পার্টিশন করার সমস্ত পদ্ধতি গণনা করে n কম বা সমান 29 এর জন্য এভাবেই চালিয়ে যাচ্ছি, তারপরে 2 টি বিন নির্বাচন করুন যেখানে আমরা 10 এর মধ্যে রেখেছি, যার ফলে 2 ওভারফ্লোভন বিনগুলিযুক্ত পার্টিশনের সংখ্যা গণনা করা হচ্ছে।
তবে এই মুহুর্তে আমাদের সাবধানতা অবলম্বন করতে হবে, কারণ আমরা ইতিমধ্যে আগের টার্মটিতে 2 টি ওভারফ্লাউন বিনযুক্ত পার্টিশনগুলি গণনা করেছি। কেবল তা-ই নয়, তবে আমরা তাদের দুটিবার গণনা করেছি। আসুন একটি উদাহরণ ব্যবহার করুন এবং 21 টি যোগফল সহ পার্টিশনটি (10,0,11) দেখুন। আগের শব্দটিতে, আমরা 10 টি বিয়োগ করেছি, বাকি 11 টির সমস্ত পার্টিশন গণনা করেছি এবং 10 টি 3 টি বিনের মধ্যে একটিতে রেখেছি। তবে এই বিশেষ বিভাজন দুটি পদ্ধতির একটিতে পৌঁছানো যেতে পারে:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
যেহেতু আমরা প্রথম বারের মধ্যেও এই পার্টিশনগুলি গণনা করেছি, 2 টি ওভারফ্লাউন বিন সহ মোট পার্টিশনের সংখ্যা 1 - 2 = -1 এর সমান, সুতরাং পরবর্তী শব্দটি যুক্ত করে আমাদের সেগুলি আরও একবার গণনা করা দরকার।
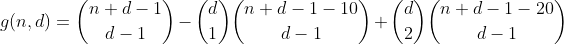
এই সম্পর্কে আরও কিছু চিন্তা করে, আমরা শীঘ্রই আবিষ্কার করলাম যে একটি নির্দিষ্ট পরিসরে একটি নির্দিষ্ট সংখ্যক ওভারফ্লাউন ডাবের একটি পার্টিশন গণনা করা হয় তা নিম্নলিখিত সারণি দ্বারা প্রকাশ করা যেতে পারে (কলাম i শব্দটি i, সারি জে পার্টিশনের প্রতিনিধিত্ব করে ওভারফ্লাউন বিন)।
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
হ্যাঁ, এটি পাস্কালস ত্রিভুজ। কেবলমাত্র আমাদের প্রথম সারিতে / কলামের মধ্যে একটি গণনা আগ্রহী, তা হ'ল শূন্য ওভারফ্লাউন বিন সহ পার্টিশনের সংখ্যা। এবং যেহেতু প্রতিটি সারির বিকল্প যোগফল কিন্তু প্রথমটির সমান 0 হয় (উদাহরণস্বরূপ 1 - 4 + 6 - 4 + 1 = 0), সুতরাং আমরা সেগুলি থেকে মুক্তি পেতে পারি এবং পেনাল্টিমেট সূত্রে পৌঁছাতে পারি।
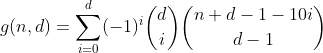
এই ফাংশনটি n এর অঙ্ক-যোগফল সহ d সংখ্যার সাথে সমস্ত সংখ্যা গণনা করে।
এখন, n এর চেয়ে কম অঙ্কের সংখ্যার কী হবে? এটি দেখানোর জন্য আমরা বাইনোমিয়াল প্লাস একটি প্ররোচিত যুক্তির জন্য একটি আদর্শ পুনরাবৃত্তি ব্যবহার করতে পারি
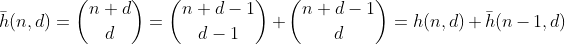
সর্বাধিক n এর মধ্যে অঙ্ক-যোগফল সহ পার্টিশনের সংখ্যা গণনা করে। এবং এইফ থেকে জি হিসাবে একই আর্গুমেন্ট ব্যবহার করে প্রাপ্ত করা যেতে পারে।
এই সূত্রটি ব্যবহার করে আমরা উদাহরণস্বরূপ 8000 থেকে 8999 পর্যন্ত ব্যবধানে ভারী সংখ্যার সন্ধান করতে পারি 1000 - f(3, 20), কারণ এই বিরতিতে হাজার সংখ্যা রয়েছে এবং আমরা ২৮ এর চেয়ে কম বা সমান সংখ্যার সংখ্যার বিয়োগ করতে হবে প্রথম অঙ্কটি ইতিমধ্যে অঙ্কের 8 টিতে অবদান রাখে এমন একাউন্টে নেওয়ার সময়।
আরও জটিল উদাহরণ হিসাবে 1234..5678 এর বিরতিতে ভারী সংখ্যার সংখ্যাটি দেখি। আমরা প্রথমে 1 এর ধাপে 1234 থেকে 1240 পর্যন্ত যেতে পারি। তারপরে আমরা 10 এর ধাপে 1240 থেকে 1300 পর্যন্ত যেতে পারি উপরের সূত্রটি আমাদের প্রতিটি বিরতিতে ভারী সংখ্যার সংখ্যা দেয়:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
এখন আমরা 100 টি পদক্ষেপে 1300 থেকে 2000 এ চলেছি:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
1000 এর পদক্ষেপে 2000 থেকে 5000 পর্যন্ত:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
এখন আমাদের আবার ধাপের আকারটি হ্রাস করতে হবে, ১০০ পদক্ষেপে 5000 থেকে 5600, 10 পদক্ষেপে 5600 থেকে 5670 থেকে এবং অবশেষে 1 এর পদক্ষেপে 5670 থেকে 5678 পর্যন্ত যেতে হবে।
পাইথন বাস্তবায়ন উদাহরণ (যা ইতিমধ্যে সামান্য অপ্টিমাইজেশন এবং পরীক্ষা পেয়েছে):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
সম্পাদনা করুন : একটি অনুকূলিত সংস্করণ দ্বারা কোডটি প্রতিস্থাপন করা হয়েছে (এটি মূল কোডের চেয়ে আরও খারাপ দেখাচ্ছে)। আমি যখন ছিলাম তখন কয়েকটি কর্নার কেসও স্থির করেছিলাম। heavy(1234, 100000000)আমার মেশিনে প্রায় এক মিলি সেকেন্ড লাগে।
