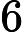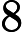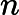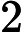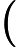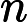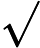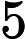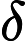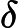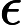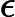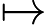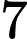উদাহরণগুলির যেখানে সমাধানের স্বতন্ত্রতা এটি সন্ধান করা আরও সহজ করে তোলে

37

জটিলতা শ্রেণীর সেই প্রবলেমগুলি নিয়ে গঠিত যা একটি বহুবর্ষ সময় ননডেটারিস্টেমনিক ট্রুরিং মেশিন দ্বারা সিদ্ধান্ত নেওয়া যেতে পারে যা সর্বাধিক একটি গণনার পথ গ্রহণ করে। অর্থাত, সমাধান, যদি কোনও হয়, এই অর্থে অনন্য । এটা অত্যন্ত অসম্ভাব্য যে সব মনে করা হয় -problems হয় কারণ দ্বারা, বীর-Vazirani উপপাদ্য এই পতন সূচিত করা হবে । $\mathsf{UP}$ $\mathsf{NP}$ $\mathsf{UP}$ $\mathsf{P}$ $\mathsf{NP}=\mathsf{RP}$

অন্যদিকে, কোন -problem হিসেবে পরিচিত -complete, যা বলে যে অনন্য সমাধান প্রয়োজন এখনও একরকম তাদের সহজ করে তোলে। $\mathsf{UP}$ $\mathsf{NP}$

আমি উদাহরণগুলি খুঁজছি, যেখানে স্বতন্ত্রতা অনুমান একটি দ্রুত অ্যালগরিদমের দিকে নিয়ে যায়।

উদাহরণস্বরূপ, গ্রাফ সমস্যাগুলির দিকে তাকানো, কোনও গ্রাফের সর্বাধিক চক্রটি কী দ্রুত খুঁজে পাওয়া যাবে (যদিও সম্ভবত এখনও ক্ষতিকারক সময়ে রয়েছে), যদি আমরা জানি যে গ্রাফটির একটি অনন্য সর্বোচ্চ চক্র রয়েছে? কীভাবে অনন্য রঙিনযোগ্যতা, অনন্য হ্যামিলটোনিয়ান পাথ, অনন্য সর্বনিম্ন আধিপত্য সেট ইত্যাদি সম্পর্কে? $k$

সাধারণভাবে, আমরা যে কোনও কমপ্লিট সমস্যার একটি অনন্য-সমাধান সংস্করণ সংজ্ঞা দিতে পারি , সেগুলি তে স্কেল করে । এটি কি তাদের কারও জন্যই পরিচিত যে স্বতন্ত্রতা অনুমিতি যুক্ত করা একটি দ্রুত অ্যালগরিদম বাড়ে? (এটি এখনও ক্ষয়ক্ষতি বজায় রেখে দেয়)) $\mathsf{NP}$ $\mathsf{UP}$

— আন্দ্রেস ফারাগো
সূত্র

7

আপনার প্রথম বাক্যটি ইউপি-র সঠিক সংজ্ঞা দেয়, তবে আপনার বাকী ইউপি-র উল্লেখগুলি পরিবর্তে সত্যিকারের প্রতিশ্রুতিতে হওয়া উচিত (ভ্যালেন্টিয়েন্ট-ওয়াজিরানি সহ)। যে কোনও উপায়ে এটি একটি খুব আকর্ষণীয় প্রশ্ন। দুটি উদাহরণ: ১) ফ্যাক্টরিং ইউপিতে, এবং এনপি-সম্পূর্ণ সমস্যার জন্য পরিচিতদের তুলনায় দ্রুত একটি অ্যালগরিদম রয়েছে (তবে ফ্যাক্টরিং এছাড়াও কোএনপি এবং এমনকি কোপও রয়েছে, সুতরাং এটি এতটা পরিষ্কার নয় যে স্বতন্ত্রতা এখানে দ্রুত অ্যালগরিদমকে অন্তর্নিহিত করছে।) 2 ) সোডোকু প্রথাগতভাবে সংজ্ঞায়িত হিসাবে প্রতিশ্রুতিবদ্ধ, তবুও সুডোকু-সমাধানের এমন কোনও পদ্ধতির কথা আমি জানি না যা প্রতিশ্রুত স্বতন্ত্রতার সুযোগ নেয় take

— জোশুয়া গ্রাচো

9

হ্যামিলটোনীয় পাথের সংখ্যার সমতাটি

( arxiv.org/pdf/1301.7250.pdf ) সময়ে পাওয়া যাবে , যখন সিদ্ধান্ত সমস্যার জন্য সর্বাধিক পরিচিত অ্যালগরিদম প্রায়

সময় নেয় ।

{1.618}^{n}

$1.618^n$

2^{n}

$2^n$

— অ্যালেক্স গোলভেনেভ

8

কোয়ান্টাম কম্পিউটিংয়ের একটি উদাহরণ এখানে: এন আইটেমগুলিতে অনুসন্ধানের সমস্যাটি বিবেচনা করুন। আপনি যদি জানেন যে ঠিক 1 টি চিহ্নিত আইটেম রয়েছে তবে আপনি এটি সঠিক কোয়ান্টাম অ্যালগরিদমের সাথে

দিয়ে খুঁজে পেতে পারেন

প্রশ্নগুলি। যদি আপনি চিহ্নিত আইটেমগুলির সংখ্যা জানেন না, তবে কোনও সঠিক কোয়ান্টাম অ্যালগরিদমের জন্য

কোয়েরি দরকার।

Θ (\sqrt{n})

$\Theta(\sqrt{n})$

n

$n$

— রবিন কোঠারি

22

3-স্যাট এ জাতীয় একটি সমস্যা হতে পারে। বর্তমানে ইউনিক 3-স্যাট-এর সর্বোত্তম উপরের সীমাটি সাধারণ 3-স্যাটের তুলনায় দ্রুততর গতিযুক্ত। (গতিবেগ তাত্পর্যপূর্ণ, যদিও ঘাতক হ্রাস ক্ষুদ্র।) অনন্য ক্ষেত্রে রেকর্ডধারক টিমন হার্টলির এই কাগজটি ।

Hertli এর এলগরিদম গুরুত্বপূর্ণ উপর তৈরী করে PPSZ অ্যালগরিদম জন্য Paturi, Pudlák, Saks, এবং Zane এর -SAT, যা আমি বিশ্বাস করি এখনও সবচেয়ে দ্রুত হয় (এছাড়াও দেখুন এই বিশ্বকোষ নিবন্ধ)। মূল বিশ্লেষণটি সাধারণ এস্যাটের তুলনায় ইউনিক এস্যাটের জন্য আরও ভাল সীমা দেখিয়েছিল যখন ; পরবর্তীকালে, হার্টলি অন্য একটি কাগজে দেখিয়েছিলেন $k$ $k \geq 5$ $k$ $k$ $k = 3, 4$ আপনি স্বতন্ত্রতা না ধরেই পিপিএসজেড অ্যালগরিদম (কিছুটা টিকড) পিপিএসজেড অ্যালগরিদমের জন্য একই সীমানা পেতে পারেন। সুতরাং, সম্ভবত স্বতন্ত্রতা সহায়তা করে এবং এটি অবশ্যই কিছু অ্যালগরিদমের বিশ্লেষণ সহজতর করতে পারে, তবে এসএটি-এর জন্য স্বতন্ত্রতার ভূমিকা সম্পর্কে আমাদের বোধগতি এখনও বাড়ছে। $k$

এমন প্রমাণ রয়েছে যে সাধারণ এস্যাট তুলনায় ইউনিক এস্যাট খুব সহজ নয় । স্ট্রং সূচকীয় সময় অনুমিতি (শেঠ) দাবি কোন নেই যেমন যে -variable -SAT মধ্যে সমাধেয় হয় প্রতিটি ধ্রুবক সময় । এটি ক্যালাব্রো, ইম্পাগলিয়াজো, কাবেনেটস এবং পাটুরির একটি কাগজে দেখানো হয়েছিল যে, যদি সেথটি ধরে রাখে, তবে একই বক্তব্যটি ইউনিক সাটের ক্ষেত্রে সত্য । এছাড়াও, যদি সাধারণ $k$ $k$ $\delta < 1$ $n$ $k$ $O^*(2^{\delta n})$ $k \geq 3$ $k$ $k$ -স্যাটের জন্য তাত্পর্যপূর্ণ সময় প্রয়োজন, অর্থাত্ কিছু রয়েছে যা সাধারণ এস্যাট সময়ে সমাধান করা যায় না , তবে ইউনিক 3-স্যাটের ক্ষেত্রে একই হওয়া উচিত। সর্বাধিক সাধারণ বিবৃতি জন্য কাগজ দেখুন। $k \geq 3, \epsilon > 0$ $k$ $O^*(2^{\epsilon n})$

(দ্রষ্টব্য: স্বরলিপি ইনপুট দৈর্ঘ্যের মধ্যে বহুপদী উপাদানগুলি দমন করে)) $O^*$

— অ্যান্ডি ড্রাগার
সূত্র

1

"অনন্য 3-স্যাট জন্য সত্য"

\mapsto

$\: \mapsto \:$ "অনন্য কে-স্যাট এর পক্ষে সত্য"

$\;\;\;\;$

হাই রিকি, আমি যা লিখেছি তাতে কোন সমস্যা দেখছি না। অনন্য 3-স্যাট সম্পর্কে সর্বশেষ দাবিটি কাগজের বিমূর্তে পাওয়া যায়।

— অ্যান্ডি ড্রকার

আহ, আমি দেখতে পাচ্ছি যে আমি যা বলছিলাম তার জন্য আলাদা আলাদা

ব্যবহার করতে হবে,

k

$k$

$\hspace{1.58 in}$ যা কেবল এটিকে বিভ্রান্ত করবে।

$\;$

16

সংক্ষিপ্ত 2- ভার্টেক্স পাথ সমস্যাটি বিচ্ছুরিত গ্রাফগুলিতে সম্প্রতি সমাধান করা (আইসিএলপি 14) এ এ। বোরক্লানড এবং টি। হুফেল্ড দ্বারা। তবে নির্বিচার সমাধানটি একটি অনন্য সমাধানের অস্তিত্বের ক্ষেত্রে। একাধিক সমাধান রয়েছে এমন ক্ষেত্রে, তারা দেখিয়েছিল যে সমস্যাটি আরপির অন্তর্গত । উল্লিখিত কাগজের লেখক হিসাবে, সমস্যাটি সাধারণ পরিস্থিতিতে পি তে আছে কিনা তা জানা যায়নি ।

— সাঈদ
সূত্র

3

আপনাকে ধন্যবাদ, এটি খুব আকর্ষণীয়। সাধারণ ক্ষেত্রে, যেখানে সমাধানটি অনন্য নয়, এটি একটি প্রাকৃতিক (বা এমনকি ব্যবহারিক) গ্রাফ সমস্যার একটি দুর্দান্ত উদাহরণ, যা এখন আরপিতে প্রমাণিত হয়েছে, তবে পি-তে রয়েছে বলে জানা যায়নি

— আন্দ্রেস ফারাগো

10

জটিলতা তত্ত্ব এবং অ্যালগরিদমের বিশ্লেষণের বাইরে, এই ধারণাটি যে একটি মাত্র সমাধান হতে পারে তা সুডোকু ধাঁধাতে সমাধানটি কেটে নেওয়ার জন্য ব্যবহৃত কিছু মান নিয়মের ভিত্তি তৈরি করে। এই নিয়মগুলিতে সাধারণত এমন উপায়গুলির সন্ধানের সাথে জড়িত থাকে যাতে ধাঁধাটির অংশগুলি দুটি বা ততোধিক সমাধান পেতে সক্ষম হতে পারে যা বাকী ধাঁধাটির সাথে যোগাযোগ করে না। এটি আসল সমাধানে ঘটতে পারে না, সুতরাং যদি এমন কোনও প্যাটার্ন যা এর কারণ হুমকির সন্ধান করে তবে এটি অবশ্যই ভেঙে যেতে হবে, সমাধানটি প্রকৃত সমাধানের মতো দেখতে সীমাবদ্ধতাগুলি কমাতে দেয়। স্বতন্ত্রতার ভিত্তিতে ছাড়ের বিধিগুলির কয়েকটি উদাহরণের জন্য http://www.brainbashers.com/sudokuuniquerectangles.asp দেখুন ।

— ডেভিড এপস্টিন
সূত্র

9

বিজার্ক্লুন্ডের অন্য একটি ফলাফল উল্লেখ করে, যদি আপনার নিশ্চিত হয় যে কোনও গ্রাফের মধ্যে কমপক্ষে একটি হ্যামিল্টোনীয় চক্র রয়েছে তবে আপনি সিদ্ধান্ত নিতে পারেন যে কোনও গ্রাফ হ্যামিলটনিয়ান আপনার চেয়ে সাধারণের চেয়ে দ্রুততর কিনা। $G$