"প্রতিবন্ধকতা কী," এই প্রশ্নের উত্তরে আমি লক্ষ করব যে প্রতিবন্ধকতা সাধারণভাবে পদার্থবিজ্ঞানের একটি বিস্তৃত ধারণা, যার মধ্যে বৈদ্যুতিক প্রতিবন্ধকতা কেবল একটি উদাহরণ।
এর অর্থ কী এবং এটি কীভাবে কাজ করে তার একটি উপলব্ধি পেতে, পরিবর্তে যান্ত্রিক প্রতিবন্ধিতা বিবেচনা করা প্রায়শই সহজ। মেঝে জুড়ে একটি ভারী পালঙ্ক ধাক্কা দেওয়ার (স্লাইড) চেষ্টা করার কথা ভাবুন।
আপনি একটি নির্দিষ্ট পরিমাণ বল প্রয়োগ করেন, এবং পালঙ্কটি আপনি কতটা ধাক্কা দেন, পালঙ্কের ওজন, তল পৃষ্ঠের ধরণ, সোফায় যে ধরণের পা ইত্যাদি ধরণের থাকে তার উপর নির্ভর করে একটি নির্দিষ্ট গতিতে স্লাইডগুলি স্লাইড হয়। এই পরিস্থিতির জন্য, কোনও যান্ত্রিক প্রতিবন্ধকতা সংজ্ঞায়িত করা সম্ভব যা আপনি কতটা কঠোর হন এবং পালঙ্কটি কীভাবে দ্রুত চলে তার মধ্যে অনুপাত দেয়।
এটি আসলে অনেকটা ডিসি বৈদ্যুতিক সার্কিটের মতো, যেখানে আপনি একটি সার্কিট জুড়ে নির্দিষ্ট পরিমাণে ভোল্টেজ প্রয়োগ করেন এবং বর্তমান মাধ্যমে এটি নির্দিষ্ট হারে প্রবাহিত হয়।
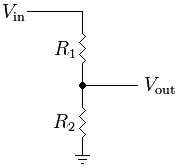
পালঙ্ক এবং সার্কিট উভয়ের ক্ষেত্রে, আপনার ইনপুটটির প্রতিক্রিয়া সহজ এবং মোটামুটি লিনিয়ার হতে পারে: একটি প্রতিরোধক যা ওহমের আইন মেনে চলে, যেখানে তার বৈদ্যুতিক প্রতিবন্ধকতা কেবলমাত্র প্রতিরোধের হয়, এবং পালঙ্কটিতে ঘর্ষণ স্লাইডার ফুট থাকতে পারে যা এটির অনুমতি দেয় আপনার বলের সাথে আনুপাতিক বেগ নিয়ে চলতে *
সার্কিট এবং মেকানিকাল সিস্টেমগুলিও অ-লাইন হতে পারে। যদি আপনার সার্কিটটিতে একটি ডায়োডের সাথে ধারাবাহিকভাবে একটি রেজিস্টার জুড়ে একটি পরিবর্তনশীল ভোল্টেজ থাকে তবে আপনি ডায়োডের সামনের দিকে অগ্রসর ভোল্টেজ অতিক্রম না করা অবধি বর্তমানের শূন্যের কাছাকাছি চলে যাবে, যেখানে ওহমের অনুসারে বর্তমান প্রতিরোধকের মধ্য দিয়ে প্রবাহিত হতে শুরু করবে আইন। একইভাবে, মেঝেতে বসে থাকা একটি পালঙ্কে সাধারণত কিছুটা স্থির ঘর্ষণ থাকে: আপনি নির্দিষ্ট পরিমাণ প্রাথমিক শক্তি দিয়ে চাপ না দেওয়া পর্যন্ত এটি চলতে শুরু করবে না। যান্ত্রিক বা বৈদ্যুতিক সিস্টেমে কোনও একক রৈখিক প্রতিবন্ধকতা নেই যা সংজ্ঞায়িত করা যায়। বরং আপনি যে সর্বোত্তম কাজটি করতে পারেন তা হ'ল পৃথক অবস্থার অধীনে প্রতিবন্ধকতার সংজ্ঞা দেওয়া। (আসল পৃথিবী আরও অনেকটা এরকম।)
এমনকি যখন বিষয়গুলি খুব স্পষ্ট এবং লিনিয়ার থাকে, তবে এটি লক্ষ্য করা গুরুত্বপূর্ণ যে প্রতিবন্ধকতা কেবল একটি অনুপাতকে বর্ণনা করে - এটি সিস্টেমের সীমাবদ্ধতা বর্ণনা করে না এবং এটি "খারাপ "ও নয়। আপনি আরও ভোল্টেজ যুক্ত করে / আরও শক্তিশালী রেখে আপনি অবশ্যই (একটি আদর্শ সিস্টেমে) যতটা বর্তমান / গতি পেতে চান তা পেতে পারেন।
মেকানিকাল সিস্টেমগুলি এসি প্রতিবন্ধকতার জন্য বেশ সুন্দর অনুভূতি দিতে পারে। কল্পনা করুন যে আপনি একটি সাইকেল চালাচ্ছেন। প্যাডেলগুলির প্রতিটি অর্ধ-চক্রের সাথে, আপনি বামদিকে চাপ দিন, ডানদিকে চাপ দিন। আপনি কেবলমাত্র এক ফুট এবং একটি পদাঙ্গুলি-ক্লিপ দিয়ে পেডেলিংয়ের কল্পনা করতে পারেন, যেমন আপনি আপনার পেডেলের প্রতিটি চক্রটি ধরে এবং টানেন। এটি অনেকটা একটি সার্কিটে এসি ভোল্টেজ প্রয়োগ করার মতো: আপনি নির্দিষ্ট প্রদত্ত ফ্রিকোয়েন্সিতে চক্রাকারে, চাপ এবং টানুন।
যদি ফ্রিকোয়েন্সি যথেষ্ট ধীর হয় - যেমন আপনি যখন বাইকে থামিয়েছিলেন, প্যাডেলগুলি নামিয়ে দেওয়ার সমস্যাটি পালঙ্কটি চাপ দেওয়ার মতো একটি "ডিসি" সমস্যা। আপনি যখন গতি বাড়ান, তবে জিনিসগুলি ভিন্নভাবে কাজ করতে পারে।
এখন, ধরুন আপনি একটি নির্দিষ্ট গতিতে সাইকেল চালাচ্ছেন, এবং আপনার বাইকটি নিম্ন, মাঝারি এবং হাই গিয়ার অনুপাত সহ একটি তিন গতি। মাঝারিটি প্রাকৃতিক অনুভূত হয়, হাই গিয়ারটি কোনও পার্থক্য তৈরির জন্য যথেষ্ট শক্তি প্রয়োগ করা কঠিন এবং কম গিয়ারে আপনি কেবল চাকাগুলিতে কোনও শক্তি স্থানান্তর না করে প্যাডেলগুলি স্পিন করেন spin এটি প্রতিবন্ধক মিলনের বিষয় , যেখানে আপনি যখন চাকাগুলিতে নির্দিষ্ট পরিমাণে শারীরিক প্রতিরোধের নির্দিষ্ট পরিমাণ উপস্থাপন করেন কেবল তখনই আপনি কার্যকরভাবে শক্তিটি স্থানান্তর করতে পারবেন - খুব বেশি নয়, খুব সামান্যও নয়। সংশ্লিষ্ট বৈদ্যুতিক ঘটনাটিও খুব সাধারণ; আপনার পয়েন্ট এ থেকে পয়েন্ট বি তে কার্যকরভাবে আরএফ শক্তি প্রেরণ করতে আপনার প্রতিবন্ধকতার সাথে মিলিত রেখাগুলি প্রয়োজন এবং আপনি যখন দুটি ট্রান্সমিশন লাইন একসাথে সংযুক্ত করেন তখন ইন্টারফেসে কিছুটা ক্ষতি হতে পারে।
পেডালগুলি আপনার পায়ের প্রতিরোধের যে পরিমাণ প্রতিরোধ সরবরাহ করে তা আপনি কতটা চাপতে চান তার সমানুপাতিক which এমনকি এসি সার্কিটগুলিতে, একটি প্রতিরোধক একটি প্রতিরোধকের মতো আচরণ করে (একটি নির্দিষ্ট বিন্দু পর্যন্ত)।
যাইহোক, একটি প্রতিরোধকের বিপরীতে, একটি সাইকেলের প্রতিবন্ধকতা ফ্রিকোয়েন্সি উপর নির্ভর করে। মনে করুন যে আপনি একটি স্টপ থেকে শুরু করে আপনার বাইকটি উচ্চ গিয়ারে রেখেছেন। এটি শুরু করা খুব কঠিন হতে পারে । তবে, একবার আপনি শুরু করার পরে, পেডালগুলি দ্বারা উপস্থাপিত প্রতিবন্ধকতা আপনি দ্রুত যেতে যেতে হ্রাস পাবে এবং একবার আপনি খুব দ্রুত যাচ্ছেন, আপনি দেখতে পাবেন যে প্যাডেলগুলি আপনার পা থেকে শক্তি শোষণ করতে খুব সামান্য প্রতিবন্ধকতা উপস্থিত রয়েছে। সুতরাং প্রকৃতপক্ষে একটি ফ্রিকোয়েন্সি-নির্ভর প্রতিবন্ধকতা (একটি বিক্রিয়া ) রয়েছে যা উচ্চ থেকে শুরু হয় এবং উচ্চতর ফ্রিকোয়েন্সি যাওয়ার সময় আপনি কম হয়ে যান।
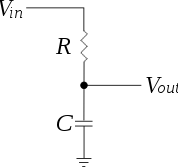
এটি অনেকটা ক্যাপাসিটরের আচরণের মতো, এবং সাইকেলের যান্ত্রিক প্রতিবন্ধকতার জন্য মোটামুটি ভাল মডেলটি ক্যাপাসিটারের সাথে সমান্তরালভাবে একটি প্রতিরোধক হবে।
ডিসি (শূন্য বেগ) এ আপনি কেবল উচ্চ ও স্থির প্রতিরোধকে আপনার প্রতিবন্ধক হিসাবে দেখেন। প্যাডেলিং ফ্রিকোয়েন্সি বাড়ার সাথে সাথে ক্যাপাসিটার প্রতিবন্ধকতা প্রতিরোধকের চেয়ে কম হয়ে যায় এবং স্রোতকে সেভাবে প্রবাহিত করতে দেয়।
অবশ্যই অন্যান্য বিভিন্ন বৈদ্যুতিক উপাদান এবং তাদের যান্ত্রিক উপমা রয়েছে **, তবে এই আলোচনার ভিত্তিতে আপনাকে সাধারণ ধারণা সম্পর্কে কিছু প্রাথমিক ধারণা দেওয়া উচিত যা আপনি মাঝে মাঝে কী দেখাতে পারে তার গাণিতিক দিকগুলি সম্পর্কে জানতে শিখেছিলেন একটি খুব বিমূর্ত বিষয় মত।
* বাছাইকারীদের কাছে একটি শব্দ: ওহমের আইন কখনই কোনও আসল ডিভাইসের জন্য সঠিক নয় এবং আসল-বিশ্বের ঘর্ষণ শক্তি কখনই গতিবেগকে বলের ঠিক সমানুপাতিক করে না। তবে, "মোটামুটি রৈখিক" সহজ। আমি এখানে সমস্ত শিক্ষামূলক এবং স্টাফ হওয়ার চেষ্টা করছি। আমাকে কিছুটা ckিল কাট
** উদাহরণস্বরূপ, একজন সূচক আপনার চাকাতে একটি বসন্ত-বোঝা রোলারের মতো কিছু যা আপনি উচ্চতর ফ্রিকোয়েন্সিতে আসার সাথে সাথে টানা যোগ করেন)