পিসিএ প্লটের একটি কদলের মতো আকারটি কী নির্দেশ করে?

Question

পাঠ্য শ্রেণিবিন্যাসের জন্য অটোনকোডারদের উপর তাদের গবেষণাপত্রে দ্বি-মাত্রিক এলএসএ (যা পিসিএর সাথে নিবিড়ভাবে সম্পর্কিত) উত্পাদিত প্লটটি প্রদর্শন করেছে: হিন্টন এবং সালখুদ্দিনভ ।

একেবারে ভিন্ন কিছু উচ্চ মাত্রিক ডেটাতে পিসিএ প্রয়োগ করা আমি একই ধরণের ত্রুটিযুক্ত প্লট পেয়েছি: (এই ক্ষেত্রে বাদে আমি সত্যিই জানতে চেয়েছিলাম কোনও অভ্যন্তরীণ কাঠামো আছে কিনা)।

আমরা যদি পিসিএতে এলোমেলো ডেটা ফিড করি আমরা একটি ডিস্ক-আকৃতির ব্লব পাই, সুতরাং এই কীলক আকারের আকৃতি এলোমেলো নয়। এটি নিজেই কিছু মানে?

Comments

আমি ধরে নিই যে সমস্ত পরিবর্তনক ধনাত্মক (বা অ-নেতিবাচক) এবং অবিচ্ছিন্ন? যদি তা হয় তবে, কিলের প্রান্তগুলি কেবলমাত্র পয়েন্ট যা অতিক্রম করে ডেটা 0 / নেতিবাচক হয়ে উঠবে। আরও, আপনি ইতিবাচক ডান-স্কিউ ভেরিয়েবলগুলির সাথে প্রদর্শিত একই প্যাটার্নটি পেতে পারেন; পর্যবেক্ষণগুলি নিম্ন প্রান্তে ছড়িয়ে পড়ে। আপনার যদি ইতিবাচক অভিন্ন র্যান্ডম ভেরিয়েবল থাকে তবে আপনি একটি (ঘোরানো) বর্গক্ষেত্রটি দেখতে পাবেন। সুতরাং আপনার দেখানো মত নিদর্শনগুলি হ'ল ডেটাতে সীমাবদ্ধতা। অন্যান্য নিদর্শনগুলি হর্সশয়ের মতো দেখাতে পারে তবে এগুলি ভেরিয়েবলের সীমাতে বাধা থাকার কারণে নয়।

— গ্যাভিন সিম্পসন

@ গ্যাভিনসিম্পসন এটি একটি মন্তব্যের চেয়ে যথেষ্ট বেশি। কেন এটি উত্তরে প্রসারিত হবে না?

— মাইক হান্টার

আমি আমার বাচ্চাদের জিজ্ঞাসা করেছি (3 এবং 4 বছর বয়সী) এই ছবিগুলি তাদের কী মনে করিয়ে দেয় এবং তারা বলেছিল এটি একটি মাছ। তাহলে সম্ভবত "মাছের মতো আকৃতি"?

— অ্যামিবা

@ গ্যাভিনসিম্পসন, ধন্যবাদ! উভয় ক্ষেত্রে ভেরিয়েবলগুলি প্রকৃতপক্ষে অ-নেতিবাচক, বট উভয় ক্ষেত্রেই তাদের পূর্ণসংখ্যার মূল্য হয়। এটি কি কিছু পরিবর্তন করে?

— macleginn

Answer 1

ভেরিয়েবলগুলি ধনাত্মক বা অ-নেতিবাচক বলে ধরে নিচ্ছেন প্রান্তের প্রান্তগুলি কেবলমাত্র পয়েন্ট যা অতিক্রম করে যথাক্রমে ডেটা 0 বা নেতিবাচক হয়ে উঠবে। যেমন বাস্তব জীবনের ডেটাগুলি সঠিকভাবে স্কিউড হওয়ার প্রবণতা রয়েছে, আমরা তাদের বিতরণের নীচের প্রান্তে পয়েন্টগুলির বেশি ঘনত্ব দেখতে পাই এবং তাই ওয়েজটির "পয়েন্ট" এ আরও বেশি ঘনত্ব।

আরও সাধারণভাবে, পিসিএ হ'ল ডেটার একটি ঘূর্ণন এবং সেই তথ্যগুলিতে সীমাবদ্ধতা সাধারণত প্রধান উপাদানগুলিতে একইভাবে প্রশ্নে প্রদর্শিত হিসাবে প্রদর্শিত হবে।

বেশ কয়েকটি লগ-সাধারণত বিতরণ করা ভেরিয়েবল ব্যবহার করে এখানে একটি উদাহরণ দেওয়া হয়েছে:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

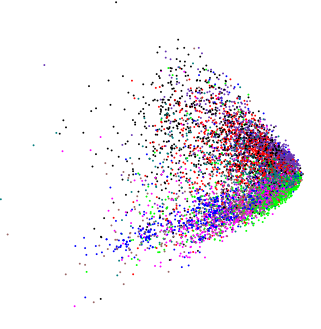
প্রথম দুটি পিসি দ্বারা আবর্তিত রোটেশনের উপর নির্ভর করে আপনি কীলক দেখতে পাবেন বা আপনি কিছুটা আলাদা সংস্করণ দেখতে পাবেন, এখানে 3 ডি ব্যবহার করে ( ordirgl()এর জায়গায় plot()) দেখান

এখানে, 3 ডি তে আমরা একাধিক স্পাইককে কেন্দ্রের ভর থেকে ছড়িয়ে পড়তে দেখছি।

গাউসিয়ান এলোমেলো ভেরিয়েবলের জন্য ( ) যেখানে প্রতিটিের একই গড় এবং ভিন্নতা রয়েছে আমরা পয়েন্টের একটি গোলক দেখতে পাই$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

এবং অভিন্ন ধনাত্মক র্যান্ডম ভেরিয়েবলের জন্য আমরা একটি ঘনক্ষেত্র দেখতে পাই see

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

এখানে নোট করুন, উদাহরণের জন্য আমি মাত্র 3 টি এলোমেলো ভেরিয়েবল ব্যবহার করে ইউনিফর্মটি দেখায় সুতরাং পয়েন্টগুলি 3d তে একটি ঘনককে বর্ণনা করে। উচ্চ মাত্রা / আরও ভেরিয়েবলের সাহায্যে আমরা 3 ডি হাইপারকিউবকে পুরোপুরি 3 ডি তে উপস্থাপন করতে পারি না এবং তাই স্বতন্ত্র "কিউব" আকারটি কিছুটা বিকৃত হয়ে যায়। অনুরূপ ইস্যুগুলি দেখানো অন্যান্য উদাহরণগুলিকে প্রভাবিত করে, তবে সেই উদাহরণগুলিতে সীমাবদ্ধতাগুলি দেখতে এখনও সহজ।

আপনার ডেটাগুলির জন্য, পিসিএর পূর্বে ভেরিয়েবলগুলির একটি লগ রূপান্তর লেজগুলিতে টানত এবং ক্ল্যাম্পড ডেটা প্রসারিত করে, আপনি যেমন লিনিয়ার রিগ্রেশনটিতে যেমন রূপান্তর ব্যবহার করতে পারেন।

অন্যান্য আকার পিসিএ প্লটে ক্রপ করতে পারে; এক ধরনের আকৃতি পিসিএ সংরক্ষিত মেট্রিক উপস্থাপনা একজন হস্তনির্মিত বস্তু এবং হিসাবে পরিচিত হয় নাল । দীর্ঘ বা প্রভাবশালী গ্রেডিয়েন্ট সহ ডেটাগুলির জন্য (ভেরিয়েবলগুলির সাথে একক মাত্রায় বর্ধিত স্যাম্পেলগুলি 0 থেকে সর্বাধিকতে বাড়ানো এবং তারপরে আবার ডেটার অংশের সাথে 0 এ কমতে এই জাতীয় নিদর্শনগুলি উত্পন্ন করার জন্য সুপরিচিত Consider

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

এটি একটি চরম ঘোড়াওয়ালা উত্পাদন করে, যেখানে অক্ষগুলির শেষের পয়েন্টগুলি মাঝখানে ফিরে বেঁকে যায়।

Comments

+1 টি। আপনার নিজের উত্তরের সাথে এখানে লিঙ্ক দেওয়া বোধগম্য হতে পারে "পর্দা / চিঠিপত্র বিশ্লেষণে" ঘোড়াগুলির প্রভাব "এবং / বা" আর্চ এফেক্ট "কী? এই উত্তরের শেষ অংশে।

— অ্যামিবা