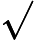এনপিআই কি পি / পলিতে থাকে?

Question

এটি অনুমান করা হয় যে যেহেতু কথোপকথনটি বোঝায় \ গণিত {পিএইচ} = \ সিগমা 2 । লাডনারের উপপাদ্যটি প্রতিষ্ঠিত করে যে যদি \ ম্যাথসফ} পি \ \ নে \ গণিত {এনপি} তবে } গণিত {এনপিআই}: = \ গণিত {এনপি} \ সেটমিনিস (\ গণিত {এনপিসি C কাপ \ গণিত {পি}) \ । তবে, প্রমাণটি \ গণিত {পি} / \ পাঠ্য {পলি general হিসাবে সাধারণীকরণ বলে মনে হচ্ছে না তাই সম্ভাবনা \ গণিত {এনপিআই \ সাবসেট \ গণিত {পি} / \ পাঠ্য {পলি} অর্থাৎ } গণিত {এনপি} \ সাবসেট \ mathsf {NPC} \ কাপ \ mathsf {P} / \ পাঠ্য {বহু} খোলা মনে হচ্ছে।$\mathsf{NP} \nsubseteq \mathsf{P}/\text{poly}$$\mathsf{PH} = \Sigma_2$$\mathsf{P} \ne \mathsf{NP}$$\mathsf{NPI} := \mathsf{NP} \setminus(\mathsf{NPC} \cup \mathsf{P}) \ne \emptyset$$\mathsf{P}/\text{poly}$$\mathsf{NPI} \subset \mathsf{P}/\text{poly}$$\mathsf{NP} \subset \mathsf{NPC} \cup \mathsf{P}/\text{poly}$

ধরে $\mathsf{NP} \nsubseteq \mathsf{P}/\text{poly}$ (বা এমনকি বহুবসায়ী স্তরক্রমটি কোনও স্তরে ভেঙে যায় না), এটি \ গণিত {এনপিআই \ \ উপসেট \ গণিত {পি} / \ পাঠ্য {বহু$\mathsf{NPI} \subset \mathsf{P}/\text{poly}$ true সত্য বা মিথ্যা হিসাবে পরিচিত? এর পক্ষে এবং বিপক্ষে কী প্রমাণ দেওয়া যেতে পারে?

Comments

সুতরাং, "এনপিতে সমস্ত সমস্যা হয় এনপি-সম্পূর্ণ বা পি-পলিতে থাকলে কী হবে"? একটি জিনিসের জন্য এটি ফ্যাক্টরিংয়ের জন্য ছোট সার্কিটগুলি বোঝায়

— সাশো নিকলভ

PS: আপনি উদ্ধৃত অংশটিতে "এটি" বানানটি পোস্ট করলে পোস্টটি আরও পঠনযোগ্য হবে। এছাড়াও আপনি ব্যবহার করতে পারেন $\mathsf{NP}\not\subseteq\mathsf{P/poly}$ স্থানে $\mathsf{NP}\not\subseteq\mathsf{P}$ আপনার ধৃষ্টতা হিসাবে।

— কাভেঃ

কোনও প্যাডিং যুক্তি কি দেখায় না যে এনপি- $\subseteq$ পি / পলি না হলে এটি ঘটতে পারে না ?

— পিটার শোর

@ পিটারশোর: আমি সম্ভবত ঘন হয়ে যাচ্ছি, তবে এটি ঠিক কীভাবে কাজ করবে?

— ভেনেসা

@ স্পার্ক: আপনি ঘন হয়ে যাচ্ছেন না ... আমি কীভাবে এটি কাজ করবে ঠিক ঠিক কাজ করিনি, এবং আমি মনে করি ফলাফলটি আমি কিছুটা ভুলভাবে বর্ণনা করেছি। তবে এখানে আমার মূল ধারণাটি। মনে করুন যে এনপি-সম্পূর্ণ সমস্যাগুলি সুবাদী সময় এবং পরামর্শে সমাধান করা যায় না। একটি এনপি-সম্পূর্ণ সমস্যা এক্স নিন, এবং এটি প্যাড করুন যাতে এটির জন্য দ্রুততম অ্যালগরিদম সবেমাত্র সাফল্যযুক্ত হয়। তারপরে এটি এনপিআই, যাতে এটি পি / পলিতে সমাধান করা যায়। এর অর্থ এনপি-সম্পূর্ণ সমস্যা এক্স পি / পলি সময়ের চেয়ে সামান্য ধীর সময়ে সমাধান করা যেতে পারে be বহুবর্ষীয় হ্রাস দ্বারা, এখন সমস্ত এনপি-সম্পূর্ণ সমস্যাগুলি পি / পলি সময়ের চেয়ে কিছুটা ধীর গতিতে সমাধান করা যেতে পারে।

— পিটার Shor

Answer 1

লাডনারের উপপাদ্যটি শানিংয়ের সাধারণীকরণের ভিত্তিতে এখানে প্যাডিং যুক্তির সম্ভাব্য বিকল্প রয়েছে। যুক্তিটি বুঝতে, আপনার এই কাগজটিতে অ্যাক্সেস থাকা দরকার (যা দুর্ভাগ্যক্রমে অনেকের জন্য বেতন দেওয়ালের পিছনে থাকবে):

উয়ে শ্যেনিং জটিলতা ক্লাসে তির্যক সেট প্রাপ্ত করার জন্য একটি অভিন্ন পদ্ধতির। তাত্ত্বিক কম্পিউটার বিজ্ঞান 18 (1): 95-103, 1982।

আমরা যে কাগজ থেকে প্রধান উপপাদ্য প্রয়োগ করা হবে এবং ভাষায় হচ্ছে এবং এবং জটিলতা শ্রেণীর হচ্ছে নিম্নরূপ:$A_1$$A_2$$\mathsf{C}_1$$\mathsf{C}_2$

• $A_1 = \varnothing$ (বা কোনও ভাষা )$\mathsf{P}$
• $A_2 = \text{SAT}$
• $\mathsf{C}_1 = \mathsf{NPC}$
• $\mathsf{C}_2 = \mathsf{NP} \cap \mathsf{P/poly}$

স্বচ্ছতার স্বার্থে, আসলে আমরা প্রমাণ হবে বোঝা ।$\mathsf{NP} \not\subseteq \mathsf{P/poly}$$\mathsf{NPI} \not\subseteq \mathsf{P/poly}$

ধৃষ্টতা অধীনে যে আমরা আছে এবং । এটি পরিষ্কার যে। এবং সীমাবদ্ধ বৈচিত্রগুলির অধীনে বন্ধ রয়েছে। কাগজে এমন একটি প্রমাণ অন্তর্ভুক্ত রয়েছে যে পুনরাবৃত্তভাবে উপস্থাপনযোগ্য (যার সুনির্দিষ্ট সংজ্ঞাটি কাগজে পাওয়া যায়) এবং যুক্তির সবচেয়ে শক্ত অংশটি প্রমাণ করে যে পুনরাবৃত্তভাবে উপস্থাপনযোগ্য।$\mathsf{NP} \not\subseteq \mathsf{P/poly}$$A_1\not\in\mathsf{C}_1$$A_2\not\in\mathsf{C}_2$$\mathsf{C}_1$$\mathsf{C}_2$$\mathsf{C}_1$$\mathsf{C}_2$

এই অনুমানগুলির অধীনে, উপপাদ্যটি ইঙ্গিত দেয় যে একটি ভাষা যা না বা ; এবং প্রদত্ত যে , এটা ঝুলিতে যে থেকে Karp-রূপান্তরযোগ্য হয় , সেইজন্য এবং । প্রদত্ত যে হয় কিন্তু কেউই নেই -complete কিংবা মধ্যে বোঝা যায় যে ।$A$$\mathsf{C}_1$$\mathsf{C}_2$$A_1\in\mathsf{P}$$A$$A_2$$A\in\mathsf{NP}$$A$$\mathsf{NP}$$\mathsf{NP}$$\mathsf{NP} \cap \mathsf{P/poly}$$\mathsf{NPI} \not\subseteq \mathsf{P/poly}$

এটি প্রমাণ করার জন্য রয়ে গেছে যে পুনরাবৃত্তভাবে উপস্থাপনযোগ্য। মূলত এর অর্থ হ'ল ডিটারমিনিস্টিক ট্যুরিং মেশিনের স্পষ্ট বর্ণনা রয়েছে যা সমস্ত সমস্ত ইনপুটগুলিতে থামে এবং এমন যে । যদি আমার যুক্তিতে কোনও ভুল হয় তবে এটি সম্ভবত এখানেই রয়েছে এবং যদি আপনাকে সত্যিই এই ফলাফলটি ব্যবহার করতে হয় তবে আপনি এটি সাবধানতার সাথে করতে চাইবেন। যাইহোক, সমস্ত বহু- (যা নির্ধারিতভাবে অনুকরণ করা যায় কারণ আমরা প্রতিটি চলমান সময় সম্পর্কে চিন্তা করি না$\mathsf{NP} \cap \mathsf{P/poly}$$M_1, M_2, \ldots$$\mathsf{NP} \cap \mathsf{P/poly} = \{L(M_k):k=1,2,\ldots\}$$M_k$) এবং সমস্ত বহুভিত্তিক, প্রদত্ত ভাষার জন্য বুলিয়ান সার্কিট পরিবারের আকারের উপরের সীমার প্রতিনিধিত্ব করে, আমি বিশ্বাস করি যে কাজ করে এমন একটি গণনা অর্জন করা কঠিন নয়। সংক্ষেপে, প্রতিটি পরীক্ষা করতে পারে যে এর সাথে সম্পর্কিত বহু- এনটিএম বহু-আকারের সার্কিটের সাথে কিছু ইনপুট স্ট্রিংয়ের দৈর্ঘ্য পর্যন্ত সমস্ত সম্ভাব্য বুলিয়ান সার্কিট অনুসন্ধান করে দেওয়া হয়। যদি চুক্তি হয়, হিসাবে কে আউটপুট, অন্যথায় এটি প্রত্যাখ্যান করে (এবং ফলস্বরূপ একটি সীমাবদ্ধ ভাষার প্রতিনিধিত্ব করে)।$M_k$$M_k$

যুক্তিটির পিছনে মূল অন্তর্নিহিততা (যা শানিংয়ের ফলাফলের অভ্যন্তরে লুকিয়ে রয়েছে) এটি হ'ল আপনি কখনই দুটি "দুর্দান্ত" জটিলতা ক্লাস (যেমন পুনরাবৃত্ত উপস্থাপনা সহকারে) একে অপরের বিরুদ্ধে বিচ্ছিন্ন হয়ে বসে থাকতে পারবেন না। জটিল শ্রেণীর "টপোলজি" এটির অনুমতি দেয় না: আপনি সর্বদা ইনপুট দৈর্ঘ্যের দীর্ঘ প্রসারিত হয়ে উভয় শ্রেণির মধ্যে একসাথে একসাথে দুটি শ্রেণির মধ্যে সঠিকভাবে একটি ভাষা তৈরি করতে পারেন can উপপাদ্যটি এবং জন্য দেখায় এবং Schöning এর জেনারেলাইজেশন আপনাকে অন্যান্য অনেক শ্রেণির ক্ষেত্রেও একই কাজ করতে দেয়।$\mathsf{P}$$\mathsf{NPC}$

Comments

এটি শানিংয়ের প্রকাশনাগুলি অনলাইনে

— আলেসান্দ্রো

ধন্যবাদ আপনার উত্তরের জন্য অনেক! মজার বিষয়টি হ'ল আমি শোওনিংয়ের উপপাদ্যটি জানতাম তবে কিছু বোকা কারণে ভেবেছিল এটি এই ক্ষেত্রে প্রযোজ্য নয়। বিটিডব্লিউ, পাঠ্যটি এমনকি বিজ্ঞান ডাইরেক্টে অবাধে উপলভ্য

— ভেনেসা

@ স্পার্ক: পি / পলি-তে নন-পুনরাবৃত্ত ভাষাগুলি অন্তর্ভুক্ত করে শনিংয়ের উপপাদ্য প্রযোজ্য না তা সন্দেহ করা বোকামি নয়। আমি মনে করি এটি সৌভাগ্যের যে আমরা এটি এনপি দিয়ে ছেদ করতে পারি এবং ফলাফলটি এখনও পেতে পারি।

— জন ওয়াটরাস

@ জন ওয়াটারস: হ্যাঁ, ঠিক এই কারণেই আমি বিভ্রান্ত হয়েছিলাম

— ভ্যানেসা

Answer 2

আমি মন্তব্যগুলিতে বর্ণিত হিসাবে একটি প্যাডিং আর্গুমেন্টের কিছু সংস্করণ লিখতে চাই। ফাঁক কেন দরকার তা আমি দেখছি না। আমরা দেখাতে চাই যে এনপি যদি পি / পলিতে না থাকে তবে পি / পলিতে এনপি-মধ্যবর্তী সমস্যা নেই।

একটি অনন্ত ফাংশন নেই যেমন যে স্যাট আকারের সার্কিট কম নেই , এবং তাই সেখানে একটি ফাংশন যে সীমাবদ্ধ নয়, বৃদ্ধি, এবং । স্যাট 'দৈর্ঘ্যের স্যাট স্ট্রিং প্যাডিং প্রয়োগ করে প্রাপ্ত ভাষা বোঝাতে যাক করতে । তারপর:$f$$n^{f(n)}$$g$$g(n)=o(f(n))$$n$$n^{g(n)}$

• স্যাট 'এনপি-তে রয়েছে (নীচে দেখুন!)
• স্যাট 'পি / পলিতে নয়: স্যাট এর জন্য সাইজের প্রদত্ত সার্কিট ', আমরা স্যাট-এর জন্য size আকারের সার্কিট পাই তবে এটি than এর চেয়ে কম কিছু ।$n^k$$n^{g(n)k}$$n^{f(n)}$$n$
• ': অসঙ্গতি ধরা যাক সেখানে সার্কিট আছে কোন পি / বহু হ্রাস স্যাট থেকে স্যাট হয় আকারের স্যাট জন্য স্যাট যার ফলে,' দরজা। যথেষ্ট বড় চয়ন করুন যে এবং । এর প্রতিটি স্যাট গেটের সর্বাধিক ইনপুট থাকে। প্যাডিং ইনপুটগুলি সরিয়ে আমরা এর স্যাট গেটগুলি একটি স্যাট গেটে ইনপুট সহ ট্রিম করতে পারি , যা আমরা ব্যবহার করে অনুকরণ করতে পারি - ফলস্বরূপ স্যাট গেটগুলি সর্বাধিক রয়েছে ইনপুট। এটি পুনরাবৃত্তি করে এবং দ্বারা চিকিত্সা করে, প্রায় আকারের সার্কিট থাকবে$C_n$$n^k$$N$$g(\sqrt{N}) > 2k$$n>N$$C_n$$n^k$$C_n$$\sqrt{n}$$C_{\sqrt{n}}$$n^{k/2}$$C_N$$O(n^k n^{k/2} n^{k/4} \dots) \approx O(n^{2k})$ যা কিছু জন্য less এর চেয়ে কম ।$n^{f(n)}$$n$

সম্পাদনা:

এর পছন্দটি কিছুটা মজাদারভাবে। আপনি যদি এনপির প্রতিশ্রুতি সংস্করণে স্যাট লাগিয়ে খুশি হন তবে এই বিটটি অপ্রয়োজনীয়।$g$

সর্বাধিক পূর্ণসংখ্যা হিসাবে সংজ্ঞায়িত করুন যে স্যাট এর জন্য দৈর্ঘ্য স্ট্রিংগুলির জন্য size আকারের কোনও সার্কিট নেই । একটি অ্যালগরিদম দ্বারা নির্ধারণ করুন যা জন্য গণনা করে এবং সময় বা যখন পরে থামে এবং এই সময়ে পাওয়া সর্বোচ্চ মানের বর্গমূলের তলটি ফেরত দেয় । সুতরাং আনবাউন্ডেড এবং এবং সময় হিসাবে গণনা করা যায় । এখন নোট করুন যে উপরের যুক্তিগুলি কেবলমাত্র স্যাট উপর নির্ভর করে যার আকারের কোনও সার্কিট নেই অসীম অনেক$f(n)$$n^{f(n)}$$n$$g(n)$$f(m)$$m=1,2,\dots$$n$$m=n$$g(n)$$\liminf g(n)/f(n)=0$$g(n)$$n$$n^{f(n)}$$n$।

Http://blog.computationalcomplexity.org/media/ladner.pdf তে যেমন স্যাট-এ গর্ত ছড়িয়ে দিয়ে একটি প্রমাণ দেখতে আগ্রহী তাও আমি খুঁজে পেয়েছি । দ্বারা NP প্রয়োজন ছাড়াই এই মোটামুটি সহজ: একটি ক্রম নেই যেমন যে কোন বর্তনী OS আকার দৈর্ঘ্যের স্যাট স্ট্রিং সনাক্ত করে ; কিছু জন্য দৈর্ঘ্যের স্ট্রিংগুলিতে সীমাবদ্ধ করুন ।$n_1<n_2<\dots$$(n_k)^k$$n$$n_{2^{2^i}}$$i$

Comments

@ জনওয়াট্রাসের উত্তর দেখার পরে, প্যাডিংয়ের মাধ্যমে লাডনারের উপপাদ্য সম্পর্কে ইমপাগলিয়াজোর প্রমাণটি স্মরণ করিয়ে দেওয়া হয়েছিল (সিএফ। ডাউনি এবং ফোর্টনো "স্বতন্ত্র হার্ড ভাষা" এর পরিশিষ্ট: cs.uchicago.edu/~fortnow/papers/uniform.pdf )। প্রকৃতপক্ষে, আপনার প্রমাণটি মূলত ইম্পাগলিয়াজোর লাডনারের প্রমাণ, তবে এই পরিস্থিতিতে মানিয়ে গেছে। ঝরঝরে!

— জোশুয়া গ্রাচো

ধন্যবাদ আপনার উত্তরের জন্য অনেক! আমি ক্ষমাপ্রার্থী আমি এটি নির্বাচন করি নি তবে আমার একটি বেছে নিতে হয়েছিল এবং ওয়াটারসের যুক্তিটি অনুসরণ করা সহজ ছিল কারণ এটি ইতিমধ্যে আমার জানা ফলাফল ব্যবহার করেছিল। এটি বেছে নেওয়ার পক্ষে বরং একটি বিষয়গত উপায় তবে আমি এর চেয়ে ভাল আর করতে পারিনি। যাইহোক, একটি আকর্ষণীয় ফলাফলে পৌঁছানোর একাধিক উপায় থাকা ভাল

— ভেনেসা

@ স্পার্ক: একেবারে - এবং আমিও ধরেছিলাম শুকিংয়ের উপপাদ্য প্রযোজ্য নয়।

— কলিন ম্যাককুইলান

Answer 3

(এনপিআই s পি / পলি) (পি এনপি)$\nsubseteq$$\implies$$\neq$

Comments

এটা উভয় পরিচিত এবং তুচ্ছ যদি পি = দ্বারা NP, তারপর । এছাড়াও এটি প্রশ্ন নয় , প্রশ্নটি আপনি যা লিখেছিলেন তার কথোপকথন এবং আমি যতদূর দেখতে পাচ্ছি নিশ্চিতভাবেই কলিন উত্তর দিয়েছিল। $\mathsf{NPI} \subseteq \mathsf{NP} = \mathsf{P} \subseteq \mathsf{P/pol}$

— সাশো নিকোলভ

প্রশ্নটি শিরোনামযুক্ত "পি / পলিতে থাকা এনপিআই" এবং মনে করেন এটি একটি যুক্তিসঙ্গত উত্তর, নিশ্চিত নয় যে এটি এনপিআইকে সাধারণত যেভাবে সংজ্ঞায়িত করা হয় (পি এনপি এর উপর নির্ভরশীল ) কারণ এটি সত্যই তুচ্ছ ... এই উত্তরটি দেয় না অন্য উত্তরের সাথে বিরোধ ...$\neq$

— vzn

আসলে এটি আরও স্পষ্টতই তুচ্ছ: যদি পি = এনপি, এনপিআই খালি থাকে। প্রশ্নটি পরিষ্কারভাবে বলা হয়েছে যে "কীভাবে পি / পলিতে এনপিআই থাকে না পি / পলিতে এনপিআই থাকে না। সুতরাং আপনার উত্তর 1) দাবি করেছে যে একটি তুচ্ছ ঘটনা একটি উন্মুক্ত সমস্যা 2) প্রশ্নটি

— সম্বোধন

পয়েন্ট সম্পর্কে কম যত্ন নিতে পারে না। শেষ বারের জন্য: আমার প্রথম মন্তব্য, কলিনের উত্তর এবং প্রশ্নটি আপনার নিজের লেখা খালি জরুরীতার তুলনায় অনেক কম তুচ্ছ এবং আরও আকর্ষণীয় কথোপকথনের সাথে সম্পর্কিত ।

— সাশো নিকোলভ

-1: কখনও কখনও হারানোর পয়েন্টটি ঠিক ঠিক মনে করে

— এলেসান্দ্রো কোসেন্টিনো