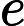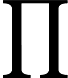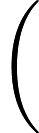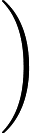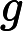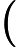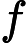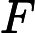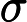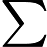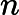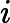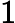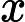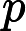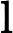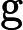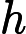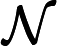বোধগম্য বন্টন এবং গাউসীয় মডেলের মধ্যে কেন স্কোয়ার ত্রুটি ক্রস-এনট্রপি হয়?

28

5.5-এ, ডিপ লার্নিং (ইয়ান গুডফেলো, যোশুয়া বেনজিও এবং অ্যারন কউরভিলি দ্বারা), এতে বলা হয়েছে

নেতিবাচক লগ-সম্ভাবনা সমন্বিত যে কোনও ক্ষতি প্রশিক্ষণ সেট দ্বারা সংজ্ঞায়িত অভিজ্ঞতা অভিজ্ঞতা এবং মডেল দ্বারা সংজ্ঞায়িত সম্ভাবনা বিতরণের মধ্যে একটি ক্রস-এনট্রপি। উদাহরণস্বরূপ, বর্গক্ষেত্রের ত্রুটিটি বোঝার জন্য অভিজ্ঞতা অভিজ্ঞতা এবং গাউসির একটি মডেলের মধ্যে ক্রস-এনট্রপি।

এগুলি কেন সমতুল্য এবং লেখকরা বিন্দুতে প্রসারিত হয় না তা আমি বুঝতে পারি না।

machine-learning normal-distribution cross-entropy

— মুফেই লি
সূত্র

32

ডেটাটি । অনুপ্রেরণামূলক বিতরণের জন্য লিখুন । সংজ্ঞা দ্বারা, কোন ফাংশন জন্য , $\mathbf{x}=(x_1, \ldots, x_n)$ $F(\mathbf{x})$ $f$

E_{F (x)} [f (X)] = \frac{1}{n} \sum_{i = 1}^{n} f (x_{i}) .

$\mathbb{E}_{F(\mathbf{x})}[f(X)] = \frac{1}{n}\sum_{i=1}^n f(x_i).$

মডেল যাক আছে ঘনত্ব যেখানে মডেলের সাপোর্টে সংজ্ঞায়িত করা হয়। ক্রস-এনট্রপি এর এবং হতে সংজ্ঞায়িত করা হয় $M$ $e^{f(x)}$ $f$ $F(\mathbf{x})$ $M$

\begin{matrix} (1) & H (F (x), M) = - E_{F (x)} [\log (e^{f (X)}] = - E_{F (x)} [f (X)] = - \frac{1}{n} \sum_{i = 1}^{n} f (x_{i}) . \end{matrix}

$H(F(\mathbf{x}), M) = -\mathbb{E}_{F(\mathbf{x})}[\log(e^{f(X)}] = -\mathbb{E}_{F(\mathbf{x})}[f(X)] =-\frac{1}{n}\sum_{i=1}^n f(x_i).\tag{1}$

ধরে নেওয়া একটি সাধারণ এলোমেলো নমুনা, এটির নেতিবাচক লগ হওয়ার সম্ভাবনা $x$

\begin{matrix} (2) & - \log (L (x)) = - \log \prod_{i = 1}^{n} e^{f (x_{i})} = - \sum_{i = 1}^{n} f (x_{i}) \end{matrix}

$-\log(L(\mathbf{x}))=-\log \prod_{i=1}^n e^{f(x_i)} = -\sum_{i=1}^n f(x_i)\tag{2}$

$(2)$ $n$ $(1)$

$p(x)$ $x$ $f$

f (x; p, σ) = - \frac{1}{2} (\log (2 π σ^{2}) + \frac{(x - p (x))^{2}}{σ^{2}}),

$f(x; p, \sigma) = -\frac{1}{2}\left(\log(2\pi \sigma^2) + \frac{(x-p(x))^2}{\sigma^2}\right),$

$(x-p(x))^2$ $1/(2\sigma^2)$ $\sigma$ $\sigma$ $\sigma$

$\sigma = \sigma(x)$

— whuber
সূত্র

1

g ()

$g ()$

f ()

$f ()$

F ()

$F ()$

σ^{2}

$\sigma^2$

k \sum_{i = 1}^{n} {(x_{i} - p (x_{i}))}^{2}

$k\sum_{i=1}^n \left (x_i - p (x_i)\right)^2$

- \frac{1}{2} \log [\sum_{i = 1}^{n} {(x_{i} - p (x_{i}))}^{2}] + h (k)

$-\frac {1}{2}\log\left [\sum_{i=1}^n \left (x_i - p (x_i)\right)^2\right] +h(k)$

F

$F$

f

$f$

হাই, আমি মনে করি এটি কেবল রৈখিক বিতরণে প্রয়োগ করা হয়। অনৈখিক বিতরণ সমস্যাগুলিতে, আমি মনে করি আমরা এখনও এমএসইকে ব্যয় হিসাবে ব্যবহার করতে পারি, তাই না?

— সিংহ লাই

5

ডিপ লার্নিং বইয়ের পাঠকদের জন্য, আমি চমৎকার গ্রহণযোগ্য উত্তরটি যুক্ত করতে চাই যে লেখকরা তাদের বক্তব্যটি 5.5.1 বিভাগে বিস্তারিতভাবে ব্যাখ্যা করেছেন যথা উদাহরণ: লিনিয়ার রিগ্রেশন সর্বাধিক সম্ভাবনা হিসাবে ।

সেখানে তারা গ্রহণযোগ্য উত্তরে উল্লিখিত বাধা ঠিকঠাক করে: