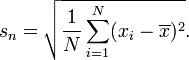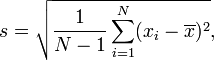মার্কিন যুক্তরাষ্ট্র ও যুক্তরাজ্যের স্কুলগুলি স্ট্যান্ডার্ড বিচ্যুতি গণনার বিভিন্ন পদ্ধতি শেখায় কেন?

Question

আমি যেমন বুঝতে পেরেছি ইউকে স্কুলগুলি ব্যবহার করে স্ট্যান্ডার্ড বিচ্যুতিটি পাওয়া যায়:

যদিও মার্কিন স্কুলগুলি পড়ায়:

(যাইহোক একটি বেসিক স্তরে)।

এটি অতীতে আমার বেশিরভাগ শিক্ষার্থীদের সমস্যার কারণ হয়ে দাঁড়িয়েছে কারণ তারা ইন্টারনেটে অনুসন্ধান করেছে, তবে ভুল ব্যাখ্যা পেয়েছে।

কেন পার্থক্য?

সাধারণ ডেটাসেটগুলি 10 টি মান বলে, ভুল পদ্ধতি প্রয়োগ করা হলে (উদাহরণস্বরূপ কোনও পরীক্ষায়) কোন ডিগ্রী ত্রুটি হবে?

Comments

আমি নিশ্চিত নই যে একটি বা অন্যটিকে 'ভুল' সূত্র হিসাবে চিহ্নিত করে বিষয়টি বোঝার উপায়। এটি ঠিক যে দ্বিতীয়টি এই অর্থে 'আরও ভাল' যে এটি সত্য প্রমিত বিচ্যুতির একটি নিরপেক্ষ অনুমানকারী। সুতরাং, যদি আপনি নিরপেক্ষ অনুমান সম্পর্কে যত্নশীল হন তবে দ্বিতীয়টিটি 'ভাল' / 'সঠিক'।

আমি সূত্রটিকে "ভুল" হিসাবে বিশুদ্ধরূপে চিহ্নিত করছিলাম যে কোনও পরীক্ষায় আপনি যদি এমন সূত্র ব্যবহার করেন যা সিলেবাস দ্বারা অনুমোদিত নয় তবে আপনি "ভুল" উত্তর দিয়ে শেষ করতে পারেন। আরও যদি মানগুলি প্রতি জনসংখ্যার নমুনা না হয় তবে অবশ্যই প্রথম সূত্রটি আরও সঠিক মান দেয়।

— আমোস

শ্রীকান্ত, আমি মনে করি না যে দ্বিতীয়টি একটি নিরপেক্ষ অনুমানক। এটা বর্গ হয় সত্য ভ্যারিয়েন্সের একটি পক্ষপাতিত্বহীন মূল্নির্ধারক। তবে, জেনসেনের বৈষম্যটি প্রতিষ্ঠিত করে যে একটি এলোমেলো ভেরিয়েবলের বক্ররেখা ফাংশনের প্রত্যাশাটি এলোমেলো ভেরিয়েবলের প্রত্যাশার ক্রিয়া হিসাবে একই নয়। সুতরাং দ্বিতীয় সূত্রটি সত্যিকারের আদর্শ বিচ্যুতির পক্ষপাতহীন অনুমানকারী হতে পারে না।

— অ্যান্ড্রু রবিনসন

ক্রস-রেফারেন্সের জন্য: এটি @ এমএসইএসকেও জিজ্ঞাসা করা হয়েছিল ...

— জেএম

দ্বারা Freedman, Pisani, & পারভেস খুব জনপ্রিয় প্রাথমিক টেক্সট ব্যবহার করে কোন মার্কিন স্কুল প্রথম সূত্র (ব্যবহার করছে ,) তাই এটি একটি মার্কিন বনাম যুক্তরাজ্যের পার্থক্য হিসাবে এই বৈশিষ্ট্য ভুল বলে মনে হয়। $s_n$

— হোবল

Answer 1

প্রথম সূত্রটি জনসংখ্যার মানক বিচ্যুতি এবং দ্বিতীয় সূত্রটি নমুনা স্ট্যান্ডার্ড বিচ্যুতি। দ্বিতীয় সূত্রটি বৈষম্যের নিরপেক্ষ অনুমানের সাথেও সম্পর্কিত - আরও তথ্যের জন্য উইকিপিডিয়া দেখুন।

আমি মনে করি (যুক্তরাষ্ট্রে) তারা হাই স্কুলে নমুনা এবং জনসংখ্যার মধ্যে পার্থক্য রাখে না। তারা অবশ্যই পক্ষপাতদুষ্ট অনুমানকারীগুলির মতো ধারণাগুলি স্পর্শ করে না।

Comments

স্ট্যান্ডার্ড বিচ্যুতিটির নিরপেক্ষ অনুমানকারী কলিনের সাধারণ ক্ষেত্রে বন্ধ ফর্ম প্রতিনিধিত্ব নেই। যা আছে তা হ'ল <i> বৈকল্পিক </ i> (এস ক্ষেত্রে ²) এর নিরপেক্ষ অনুমানক। লক্ষণীয় যে উভয়ই জনসংখ্যার বৈচিত্রের ধারাবাহিক অনুমানকারী - এবং তাই অবিচ্ছিন্ন ম্যাপিং উপপাদ্য দ্বারা, স্ট্যান্ডার্ড বিচ্যুতির দুটি অনুমানকারী। সম্পর্কিত পয়েন্টটি হ'ল _n ² এর ² এর চেয়ে কম এমএসই রয়েছে। পক্ষপাতদুষ্টতা চাপিয়ে দেওয়ার অতিরিক্ত সুবিধাটি তর্কযোগ্য।

— সকাল

@ তীর্থঙ্কর - আমার খুব slালু আমি উত্তর কিছুটা পরিবর্তন করেছি। ধন্যবাদ।

— csgillespie

যতদূর আমার মনে আছে, আমাকে জিসিএসই গণিত ও বিজ্ঞানে 'নমুনা' গণনা শেখানো হয়েছিল (বয়স 14-16) এবং জনসংখ্যা এবং নমুনাগুলির মধ্যে পার্থক্য এবং তাদের সম্পর্কিত প্রকরণের ব্যবস্থাগুলি এ-লেভেলে আচ্ছাদন করা হয়েছিল (যদিও গভীরতার সাথে নয়) বয়স 16-18)। সুতরাং আমি নিশ্চিত নই যে এটি সাধারণ ইউকে / মার্কিন পার্থক্য।

— ফ্রেইয়া হ্যারিসন

Answer 2

কারণ কেউ এখনও চূড়ান্ত প্রশ্নের উত্তর দেয়নি - যথা, দুটি সূত্রের মধ্যে পার্থক্যকে মাপ দিতে - আসুন এটি যত্ন নেওয়া উচিত।

অনেক কারণেই, তাদের পার্থক্যের চেয়ে তাদের অনুপাতের ক্ষেত্রে স্ট্যান্ডার্ড বিচ্যুতির তুলনা করা উপযুক্ত । অনুপাত হয়

$$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$$

বর্গমূলের জন্য (বিকল্প) টেলর সিরিজটি কাটা হিসাবে প্রায় অনুমান করা যেতে পারে, নির্দেশ করে ত্রুটিটি অতিক্রম করতে পারে না =1/(8এন2)। এটি প্রতিষ্ঠিত করে যেN2বা তার চেয়ে বড় হয়েগেলে আনুমানিক পরিমাণটি যথেষ্ট ভাল (আমাদের উদ্দেশ্যে) ভালহয়।$|\binom{1/2}{2}N^{-2}|$$1 / (8 N^2)$$N$$2$

এটি অবিলম্বে যে দুটি এসডি অনুমান একে অপরের 10% (প্রায়) এর মধ্যে থাকে যখন একবার 5 ছাড়িয়ে যায় , 5% এর মধ্যে N একবার 10 ছাড়িয়ে যায় , ইত্যাদি। স্পষ্টতই, অনেক উদ্দেশ্যে এই তফাতগুলি এত ছোট যে কোনও সূত্রটি ব্যবহৃত হয় তা বিবেচনা করে না, বিশেষত যখন এসডি ডেটার বিস্তারকে বর্ণনা করার জন্য বা অর্ধ-পরিমাণগত তৈরির উদ্দেশ্যে করা হয়$N$$5$$N$$10$ প্রসারণের মূল্যায়ন বা ভবিষ্যদ্বাণী করার জন্য করা হয় (যেমন 68-95 ব্যবহারের ক্ষেত্রে) -99.7 থাম্বের নিয়ম)। তুলনা করার সময় তাত্পর্যগুলি আরও কম গুরুত্বপূর্ণএসডি, যেমন দুটি ডেটাসেটের স্প্রেডের সাথে তুলনা করার সময়। (যখন ডেটাসেটগুলি সমান হয়, তফাতগুলি কার্যকরভাবে পুরোপুরি অদৃশ্য হয়ে যায় এবং উভয় সূত্রই অভিন্ন সিদ্ধান্তে নিয়ে যায়)) তাত্পর্যপূর্ণভাবে, এগুলি যুক্তিগুলির ফর্ম যা আমরা প্রারম্ভিক শিক্ষার্থীদের শেখানোর চেষ্টা করছি, তাই যদি শিক্ষার্থীরা কোন সূত্রটি ব্যবহার করবেন সে সম্পর্কে উদ্বিগ্ন হয়ে পড়ছে, এটি একটি চিহ্ন হিসাবে গ্রহণ করা যেতে পারে যে পাঠ্য বা শ্রেণি আসলে কী গুরুত্বপূর্ণ তা জোর দিতে ব্যর্থ হচ্ছে।

আমরা খুব ছোট এর ক্ষেত্রে কিছুটা মনোযোগ দিতে চাই । এখানে লোকেদের z টেস্টের পরিবর্তে টি টেস্ট ব্যবহার করা যেতে পারে । সেক্ষেত্রে স্ট্যান্ডার্ড বিচ্যুতির যে কোনও সূত্র কারও টেবিল বা সফ্টওয়্যার দ্বারা ব্যবহৃত হয় তা নিয়োগ করা অপরিহার্য । (এটি একটি ফর্মুলার ভুল বা সঠিক হওয়ার বিষয় নয়; এটি কেবল একটি ধারাবাহিকতার প্রয়োজনীয়তা)) বেশিরভাগ সারণী এস ব্যবহার করে না, এস এন : প্রাথমিক পাঠ্যক্রমের ক্ষেত্রে এটিই একটি জায়গা যেখানে পাঠ্য এবং শিক্ষককে কোনটি সম্পর্কে পরিষ্কার হওয়া দরকার সূত্র ব্যবহার করতে।$N$$t$$z$$s$$s_n$

Answer 3

এটি বেসেলের সংশোধন । মার্কিন সংস্করণ নমুনা স্ট্যান্ডার্ড বিচ্যুতির সূত্র দেখাচ্ছে is , যেখানে ইউ সংস্করণের থেকে উচ্চতর নমুনার স্ট্যান্ডার্ড ডেভিয়েশন ।

Answer 4

আমি নিশ্চিত নই যে এটি খালি মার্কিন বনাম ব্রিটিশ ইস্যু। এই পৃষ্ঠার বাকি একটি FAQ আমি লিখেছি থেকে উদ্ধৃত করা হয়। ( Http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 )।

ডিনোমিনেটরে কীভাবে এসডিটি এন -1 এর সাথে গণনা করা যায়

1. প্রতিটি মান এবং নমুনা গড়ের মধ্যে পার্থক্যের বর্গাকার গণনা করুন।

2. এই মানগুলি যোগ করুন।

3. যোগফলটিকে n-1 দিয়ে ভাগ করুন। ফলাফলটিকে রূপান্তর বলা হয়।

4. স্ট্যান্ডার্ড বিচ্যুতি পেতে বর্গমূল নিন।

এন -১ কেন?

একটি আদর্শ বিচ্যুতি গণনা করার সময় কেন এন-এর পরিবর্তে এন -1 দ্বারা ভাগ করবেন? পদক্ষেপ 1 এ, আপনি প্রতিটি মান এবং সেই মানগুলির গড়ের মধ্যকার পার্থক্যটি গণনা করেন। আপনি জনসংখ্যার প্রকৃত গড় জানেন না; আপনারা জানেন সমস্ত আপনার নমুনার গড়। নমুনাটির অর্থ জনসংখ্যার গড় সমান হওয়ার ক্ষেত্রে বিরল ক্ষেত্রে বাদে, তথ্যটি নমুনা গড়ের তুলনায় প্রকৃত জনসংখ্যার চেয়ে বেশি হবে। সুতরাং আপনি দ্বিতীয় ধাপে যে মানটি গণনা করছেন তা সম্ভবত কিছুটা ছোট (এবং বৃহত্তর হতে পারে না) যদি আপনি প্রকৃত জনসংখ্যাটি ধাপ 1-এ ব্যবহার করেন তবে এটির জন্য, এন -1 দ্বারা ভাগ করুন এনভি তুলনায় এটি বেসেল সংশোধন বলা হয়।

তবে এন -১ কেন? আপনি যদি নমুনার অর্থটি জানতেন এবং মানগুলির ব্যতীত সমস্তগুলি, তবে আপনি শেষের মানটি কী হতে হবে তা গণনা করতে পারেন। পরিসংখ্যানবিদরা বলেছেন স্বাধীনতার এন -1 ডিগ্রি রয়েছে।

এসডি কখন এন -1 এর পরিবর্তে এন এর ডিনমিনেটরের সাথে গণনা করা উচিত?

পরিসংখ্যানের বইগুলি প্রায়শই এসডি গণনার জন্য দুটি সমীকরণ দেখায়, একটি এন ব্যবহার করে, এবং অন্যটি ডিনোমিনেটরে এন-1 ব্যবহার করে। কিছু ক্যালকুলেটর দুটি বোতাম আছে।

এন -1 সমীকরণটি সাধারণ পরিস্থিতিতে ব্যবহার করা হয় যেখানে আপনি তথ্যের একটি নমুনা বিশ্লেষণ করছেন এবং আরও সাধারণ সিদ্ধান্তে আসতে চান। এসডিটি এইভাবে গণনা করা হয় (ডিনোমিনেটরে এন -1 সহ) সামগ্রিক জনসংখ্যার এসডিটির মান সম্পর্কে আপনার সেরা অনুমান।

আপনি যদি কোনও নির্দিষ্ট উপাত্তের প্রকারের পরিমাণটি কেবলমাত্র প্রমাণ করতে চান, এবং আরও বিস্তৃত সিদ্ধান্ত নেওয়ার জন্য এক্সট্রপোলেট করার পরিকল্পনা না করেন, তবে আপনি ডিনোমিনেটরে এন ব্যবহার করে এসডি গুনতে পারেন। ফলাফল এসডি হ'ল সেই নির্দিষ্ট মানগুলির এসডি। আপনি যদি জনসংখ্যার যে পয়েন্টগুলি আঁকেন সেখানকার এসডি অনুমান করতে চান তবে এসডিটিকে এইভাবে গণনা করার কোনও অর্থ নেই। কোনও জনগোষ্ঠীর থেকে নমুনা না থাকলে, সাধারণ সিদ্ধান্তে নেওয়ার ইচ্ছা নেই তখনই ডিনোমিনেটরে এন ব্যবহার করার অর্থ হয়।

বিজ্ঞানের লক্ষ্য প্রায় সর্বদা জেনারেলাইজ করা, তাই ডিনোমিনেটরে n এর সাথে সমীকরণটি ব্যবহার করা উচিত নয়। একমাত্র উদাহরণটি যেখানে এটি বোধগম্য হতে পারে তা নিয়েই ভাবতে পারি পরীক্ষার স্কোরগুলির মধ্যে পার্থক্যের পরিমাণ নির্ধারণ করতে। তবে প্রতিটি স্কোরের একটি স্ক্র্যাটারপ্লট বা ফ্রিকোয়েন্সি বিতরণ হিস্টোগ্রাম প্রদর্শন করা আরও ভাল।

Comments

আমি এটিকে পরামর্শ দিচ্ছিলাম না, আমি কেবল কৌতূহলী ছিলাম যে কেন এইরকম পার্থক্য দেখা দিয়েছে, ভুল উপদেশ অনুসরণের ফলে কোন ধরণের ত্রুটি ঘটতে পারে এবং আমি আমার শিক্ষার্থীদের যে পার্থক্যটি দিতে পারি তার সুনির্দিষ্ট ব্যাখ্যা ছিল কিনা whether ।

— আমোস

@ হারভে - লিঙ্কটি মারা গেছে

— বাক্সেক্স 11:30

@ বাক্স্স .. এটি দেখানোর জন্য ধন্যবাদ। সংশোধন করা হয়েছে।

— হার্ভে মোটুলস্কি

Answer 5

যেহেতু N ডেটা সেটে পয়েন্টের সংখ্যা, সুতরাং কেউ যুক্তি দিতে পারে যে গড় হিসাবে গণনা করে একজনের দ্বারা নির্ধারিত তথ্যগুলিতে স্বাধীনতার ডিগ্রি হ্রাস পেয়েছে (যেহেতু একজন ডেটা সেটের উপর নির্ভরশীলতার পরিচয় দিয়েছিল) সুতরাং এনকে ব্যবহার করা উচিত -1 যখন কোনও ডেটা সেট থেকে স্ট্যান্ডার্ড বিচ্যুতি অনুমান করার জন্য যার আগে কোনওটির গড় অনুমান করতে হয়েছিল।