বায়েসের উপপাদ্য কী?

36

বায়েসের উপপাদ্য সম্পর্কিত মূল ধারণাগুলি কী ? আমি জটিল গাণিতিক স্বরলিপিগুলির কোনও অনুপাতের জন্য বলছি না।

probability bayesian theory

— user333
সূত্র

4

সম্পর্কিত: stats.stackexchange.com/questions/22/…

— শেন

3

আমি এই লিঙ্কটিকে এক ধরণের নিম্ন-স্তরের-ব্যাখ্যা হিসাবেও বলতে চাই

— স্টেফেন

1

বেয়েসের উপপাদ্যটি দর্শনের উপস্থাপনা ছাড়াই বিড়বিড় হতে পারে often ম্যাথগুলিতে প্রায়শই। বায়েশিয়ান সম্ভাব্যতার জন্য সম্ভাব্যতা স্কোয়ার বা সম্ভাবনা গাছ ব্যবহার করবেন না কেন? যখন নতুন ডেটা আসে তখন তা নমুনার কিছু জায়গা বন্ধ করে দেয় (উদাহরণস্বরূপ, কোনও রোগের জন্য ইতিবাচক পরীক্ষা করা নেগেটিভ হওয়া বন্ধ করে দেওয়া হয়)। তারপরে নমুনা স্থানটি সম্ভাব্য-পরীক্ষিত পরীক্ষাগুলির কেবলমাত্র একটি উপ-সেট হয়ে যায়, সম্ভবত- এবং একমাত্র এটি বিবেচনা করে। আমার যে অসুবিধা হচ্ছে তা হ'ল বেইসকে বিযুক্ত সম্ভাবনার পরিবর্তে সম্ভাব্যতা বিতরণে প্রয়োগ করা। গণিতগুলি নরকীয়ভাবে ভয়াবহ!

22

বয়েসের উপপাদ্য হ'ল সম্ভাবনা তত্ত্বের তুলনামূলক সহজ, তবে মৌলিক ফলাফল যা কিছু শর্তাধীন সম্ভাবনার গণনার জন্য অনুমতি দেয়। শর্তাধীন সম্ভাবনাগুলি হ'ল কেবল সেই সম্ভাবনা যা অন্য ইভেন্টের সম্ভাবনার উপর একটি ইভেন্টের প্রভাব প্রতিফলিত করে।

সহজ কথায়, এটি সবচেয়ে বিখ্যাত আকারে বলা হয়েছে যে নতুন ডেটা ( পি (এইচ। ডি) ; উত্তরোত্তর সম্ভাবনা বলা হয়) দেওয়া হাইপোথিসিসের সম্ভাবনা নিম্নলিখিত সমীকরণের সমান: অনুমান করা তথ্যের দ্বারা পর্যবেক্ষণ করা তথ্যের সম্ভাবনা ( পি (ডি | এইচ) ; শর্তসাপেক্ষ সম্ভাবনা বলা হয়), নতুন প্রমাণ ( পি (এইচ) ; এইচ এর পূর্ব সম্ভাবনা বলা হয় ) এর আগে তত্ত্বের সম্ভাব্যতার সত্য হওয়ার বার , সেই তথ্যটি দেখার সম্ভাবনা দ্বারা বিভক্ত, পিরিয়ড ( পি (ডি ); ডি এর প্রান্তিক সম্ভাবনা বলা হয়)।

সাধারণত, সমীকরণটি এর মতো দেখায়:

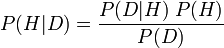
$বিকল্প পাঠ$

বয়েস উপপাদ্যের তাত্পর্যটি মূলত এর যথাযথ ব্যবহারের কারণেই সম্ভাবনা নিয়ে চিন্তাভাবনার স্কুলগুলির মধ্যে একটি বিতর্ক হিসাবে দেখা যায়। একটি বিষয়গত বায়েশিয়ান (যা বিশ্বাসের সাপেক্ষিক ডিগ্রি হিসাবে সম্ভাবনা ব্যাখ্যা করে) কাছে বয়েসের উপপাদ্য তত্ত্ব পরীক্ষা, তত্ত্ব নির্বাচন এবং অন্যান্য অনুশীলনের জন্য ভিত্তিটি সরবরাহ করে, তাদের বিষয়গত সম্ভাবনার বিচারগুলি সমীকরণে প্লাগ করে এবং এর সাথে চালিয়ে যায়। একটি ঘনত্ববাদী (যেটি সম্ভাবনাকে আপেক্ষিক ফ্রিকোয়েন্সি সীমাবদ্ধ হিসাবে ব্যাখ্যা করে ) এর কাছে বয়েসের উপপাদ্যটির এই ব্যবহারটি অপব্যবহার এবং তারা পরিবর্তে অর্থবহ (অ-বিষয়গত) প্রিরিয়ার ব্যবহার করার চেষ্টা করে (সম্ভাব্যতার আরও একটি ব্যাখ্যার অধীনে উদ্দেশ্যমূলক বায়েশিয়ানরাও করেন)।

— জন এল টেলর
সূত্র

1

ভাল উত্তর. আমার একটি ছোট বাচ্চা আছে: "সাবজেক্টিভ" এবং "অবজেক্টিভ" শব্দের ব্যবহার বেশ উপযুক্ত নয়, কারণ কোনও পদ্ধতিই "উদ্দেশ্য" নয়। আমি আরও বলি যে ঘন ঘন এবং "উদ্দেশ্যমূলক" বায়েশিয়ানরা কিছু নিয়ম বা মান ব্যবহার করে কেবল তাদের সম্ভাব্যতা বন্টন করতে পারে। সুতরাং নির্দিষ্ট মামলার জন্য হাতছাড়া করার পরিবর্তে, ঘন ঘনবাদী / উদ্দেশ্য বায়েশিয়ান "ডিফল্ট" পছন্দগুলি প্রয়োগ করবেন (এভাবে তাদের সাবজেক্টিভিটি লুকিয়ে রাখবেন)।

— সম্ভাব্যতাব্লোগিক

যদি আপনি প্রকৃত মূল্যবান কিছু পরিমাপ করেন (6 বছরের বাচ্চাদের উচ্চতা বলুন), তবে পি (ডি) কী? এটি কি ডেটা পিডিএফ? কোন ক্ষেত্রে আপনি কেবল উত্তর-পূর্বের দিকটি গণনা করছেন:

?

P (x | H | D) = \frac{P (x | D | H) P (x | H)}{P (x | D)}

$P(x|H|D) = \frac{P(x|D|H)P(x|H)}{P(x|D)}$

— nnot101

13

আমি দুঃখিত, তবে এখানে কিছুটা বিভ্রান্তি রয়েছে বলে মনে হয়: বাইয়েসের উপপাদ্য খুব নিকটবর্তী বায়েশিয়ান- ফ্রিকোয়েনসিবাদী বিতর্কের আলোচনায় আসেনি । এটি এমন একটি উপপাদ্য যা উভয় বিদ্যালয়ের চিন্তার সাথে সামঞ্জস্যপূর্ণ (প্রদত্ত যে এটি কোলমোগোরভের সম্ভাব্য অক্ষরের সাথে সামঞ্জস্যপূর্ণ)।

অবশ্যই বায়েসের উপপাদ্য বায়েশিয়ান পরিসংখ্যানের মূল, তবে উপপাদ্যটি সর্বজনীন। ঘন ঘন এবং বায়েশীয়দের মধ্যে সংঘর্ষ বেশিরভাগের সাথে সম্পর্কিত যে পূর্বের বিতরণগুলি কীভাবে সংজ্ঞায়িত করা যায় বা কীভাবে সংজ্ঞায়িত করা যায়।

সুতরাং, যদি প্রশ্নটি বয়েসের উপপাদ্য (এবং বায়েশিয়ান পরিসংখ্যান নয়) সম্পর্কে:

বায়েসের উপপাদ্যটি নির্দিষ্ট করে দেয় যে কীভাবে কেউ নির্দিষ্ট শর্তাধীন সম্ভাবনা গণনা করতে পারে। উদাহরণস্বরূপ কল্পনা করুন যে আপনি জানেন: এক্স পি (এ | এক্স) রোগ হওয়ার কারণে কারও কারও উপসর্গ হওয়ার সম্ভাবনা রয়েছে; এক্স পি (এক্স) রোগে আক্রান্ত হওয়ার কারও সাধারণের সম্ভাবনা; সাধারণভাবে কারও কারও সম্ভাবনা হ'ল উপসর্গ এ পি (এ) থাকে। এই 3 টি টুকরো তথ্যের সাহায্যে আপনি এক্স রোগের কারও সম্ভাবনা গণনা করতে পারেন, প্রদত্ত যে তাদের সিম্পটম এ পি (এক্স | এ) রয়েছে।

— ডেভ কেলেন
সূত্র

1

আমি আপনার প্রাথমিক অনুচ্ছেদের সাথে একমত নই কারণ প্রশ্নগুলি বয়েস উপপাদ্যের ধারণা সম্পর্কে জিজ্ঞাসা করে। ফ্রিকোয়েনসিস্ট-বায়েশিয়ান বিতর্ক প্রশ্নের এই অংশের সাথে প্রাসঙ্গিক । কোলমোগোরভ অ্যাকোরিওমগুলি "বর্ধিত যুক্তির মতো সম্ভাবনা" অক্ষরূপের মতো বায়েস উপপাদ্যকে তেমন ধারণামূলক গুরুত্ব দেয় না।

— সম্ভাব্যতাব্লোগিক

8

বেয়েসের উপপাদ্য শর্তসাপেক্ষ সম্ভাবনা কে অন্য শর্তযুক্ত সম্ভাবনা ঘোরানোর একটি উপায় । $P(A|B)$ $P(B|A)$

কারওর জন্য হোঁচট খাওয়ার অর্থ । সম্ভাব্য ইভেন্টগুলির স্থান হ্রাস করার একটি উপায় এটি কেবলমাত্র সেই ঘটনাগুলিতে বিবেচনা করে যেখানে স্পষ্টভাবে ঘটে (বা সত্য)। সুতরাং উদাহরণস্বরূপ, ছয়, দেখানো একটি নিক্ষিপ্ত, ন্যায্য, পাশা জমিগুলি সম্ভাব্যতা ১/ is, তবে একটি পাশ্ব জমি ছয়টি একটি সমান সংখ্যায় অবতরণ করার সম্ভাবনা রয়েছে, , 1/3। $P(B|A)$ $A$ $P(\mbox{dice lands six})$ $P(\mbox{dice lands six}|\mbox{dice lands even})$

আপনি বায়েসের উপপাদ্যটি নীচের মতো করে নিতে পারেন। শর্তাধীন সম্ভাবনার অনুপাত সংজ্ঞা দিয়ে শুরু করুন:

$P(B|A) = \frac{P(AB)}{P(A)}$

$P(AB)$ $A$ $B$ $P(A)$ $A$

$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$ $AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$ $P(AB)$

$P(AB) = P(A|B)P(B)$

ওহে প্রেস্টো:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

শর্তসাপেক্ষ সম্ভাবনাটি এভাবে ঘুরিয়ে দেওয়ার জন্য বিন্দুটি কী তা বোঝার জন্য, কারওর একটি লক্ষণ রয়েছে যে প্রদাহ হওয়ার সম্ভাবনাটি অনুমান করার চেষ্টা করার সাধারণ উদাহরণ বিবেচনা করুন, অর্থাৎ, আমরা জানি যে তাদের একটি লক্ষণ রয়েছে - আমরা ঠিক পারি এটি দেখুন - তবে তাদের কোনও রোগ আছে কিনা এবং তা নির্ণয় করতে হবে কিনা তা আমরা নিশ্চিত হতে পারি না। আমি সূত্রটি দিয়ে শুরু করব এবং ফিরে আসব।

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

সুতরাং এটি কার্যকর করার জন্য, আপনাকে লক্ষণটির পূর্ব সম্ভাবনা, রোগের পূর্ব সম্ভাবনা (যেমন, লক্ষণ এবং রোগ কতটা সাধারণ বা বিরল) এবং আপনার কারও লক্ষণ রয়েছে এমন সম্ভাবনাও জানা দরকার যা আমরা জানি যে কারওর রয়েছে একটি রোগ (যেমন ব্যয়বহুল সময় গ্রহণকারী ল্যাব পরীক্ষার মাধ্যমে)

এটি এর থেকে অনেক বেশি জটিল হয়ে উঠতে পারে, উদাহরণস্বরূপ, আপনার যদি একাধিক রোগ এবং লক্ষণ থাকে তবে ধারণাটি একই। আরও সাধারণভাবে, যদি আপনার কারণগুলির (যেমন, রোগ) এবং প্রভাবগুলির (যেমন, লক্ষণগুলি) মধ্যে সম্পর্কের সম্ভাবনা তত্ত্ব থাকে তবে বেইসের উপপাদ্যটি প্রায়শই উপস্থিত হয় এবং আপনার পিছনের দিকে তর্ক করা দরকার (যেমন, আপনি কিছু লক্ষণ দেখতে পান যা থেকে আপনি চান) অন্তর্নিহিত রোগ অনুমান করা)।

— AndyF
সূত্র

5

দুটি চিন্তাভাবনা মূলত বিদ্যালয়টি হ'ল: পরিসংখ্যানবাদী এবং বায়েশিয়ান ।

বয়েস উপপাদ্যটি পরবর্তীকালের সাথে করা এবং এটি বোঝার একটি উপায় হিসাবে দেখা যায় যে কোনও তত্ত্ব সত্য হওয়ার সম্ভাবনাটি নতুন প্রমাণের দ্বারা কীভাবে প্রভাবিত হয়। এটি শর্তযুক্ত সম্ভাবনা হিসাবে পরিচিত। আপনি গণিতে হ্যান্ডেল পেতে এটি দেখতে চাইতে পারেন ।

— টনি ব্রেকিয়াল
সূত্র

4

আমি আপনাকে একটি খুব স্বজ্ঞাত অন্তর্দৃষ্টি দিতে দিন। মনে করুন আপনি একটি মুদ্রা 10 বার টস করছেন এবং আপনি 8 টি মাথা এবং 2 টি লেজ পেয়েছেন। আপনার মনে যে প্রশ্নটি আসবে তা হ'ল এই মুদ্রাটি মাথার দিকে পক্ষপাতদুষ্ট কিনা।

এখন আপনি যদি প্রচলিত সংজ্ঞা বা সম্ভাবনার ঘন ঘন দৃষ্টিভঙ্গি অনুসরণ করেন তবে আপনি বলতে পারেন যে মুদ্রা পক্ষপাতদুষ্ট এবং এটি একটি ব্যতিক্রমী ঘটনা। সুতরাং আপনি উপসংহারে পৌঁছে যাবেন যে পরবর্তী টসে মাথা পাওয়ার সম্ভাবনাও 50%।

তবে ধরুন আপনি বায়েশিয়ান। আপনি প্রকৃতপক্ষে ভাববেন যেহেতু আপনি খুব বেশি সংখ্যক মাথা পেয়েছেন, তাই মুদ্রার মাথা দিকের দিকে পক্ষপাত রয়েছে। এই সম্ভাব্য পক্ষপাত গণনা করার পদ্ধতি রয়েছে। আপনি সেগুলি গণনা করতেন এবং তারপরে আপনি যখন পরবর্তী সময় মুদ্রাটি টস করবেন, আপনি অবশ্যই একটি প্রধানকে ডাকবেন।

সুতরাং, বায়েশিয়ান সম্ভাবনা হ'ল আপনার পর্যবেক্ষণ করা ডেটার ভিত্তিতে আপনি যে বিশ্বাস বিকাশ করেন সে সম্পর্কে। আমি আশা করি এটি যথেষ্ট সহজ ছিল।

— htrahdis
সূত্র

অবশ্যই, কেবল ফলাফলের চেয়ে কয়েনের টসে আরও বেশি ডেটা রয়েছে - একটি বুদ্ধিমান বেইসিয়ান সম্ভবত অতীতের তথ্যের ওজনের কারণে এবং মুদ্রা এবং মুদ্রার ফ্লিপটি ফর্সা দেখায় বলে সম্ভবত বেট করবে। সম্ভবত, যদি না আপনি মুদ্রা দেখতে পাচ্ছেন না, বা মুদ্রাটি উল্টানো হচ্ছে being এই ক্ষেত্রে আপনি এমনকি

— এটিও

3

বয়েসের উপপাদ্য দুটি ধারণা সম্পর্কিত: সম্ভাবনা এবং সম্ভাবনা। সম্ভাবনা বলে: এই মডেলটি দেওয়া, এগুলি ফলাফল। সুতরাং: একটি ন্যায্য মুদ্রা দেওয়া, আমি 50% সময় পেয়ে যাব। সম্ভাবনা বলে: এই ফলাফলগুলি দেওয়া, আমরা মডেল সম্পর্কে এটি বলতে পারি। সুতরাং: আপনি যদি 100 বার একটি মুদ্রা টস করেন এবং 88 টি মাথা পান (পূর্ববর্তী উদাহরণটি বেছে নিতে এবং এটি আরও চূড়ান্ত করতে), তবে ন্যায্য মুদ্রার মডেলটি সঠিক হওয়ার সম্ভাবনা এত বেশি নয়।

বয়েসের উপপাদ্য চিত্রিত করার জন্য ব্যবহৃত একটি আদর্শ উদাহরণ হ'ল একটি রোগের পরীক্ষা করার ধারণা: যদি আপনি একটি পরীক্ষা করেন তবে জনসংখ্যার 10000 জন 1 জনের একটি রোগের জন্য 95% সঠিক এবং আপনি ইতিবাচক পরীক্ষা করেন, তবে এর সম্ভাবনাগুলি কী? আপনার কি রোগ আছে?

নিষ্পাপ উত্তর 95%, তবে এটি 10000 লোকের মধ্যে 9999 টির মধ্যে 5% পরীক্ষার একটি মিথ্যা ইতিবাচক বিষয়টিকে অগ্রাহ্য করে। সুতরাং আপনার এই রোগ হওয়ার সম্ভাবনাগুলি 95% এর চেয়ে অনেক কম lower

আমার "অসম্ভব সম্ভাবনা" অস্পষ্ট বাক্যাংশটি ইচ্ছাকৃতভাবে ব্যবহার করা। সম্ভাবনা / সম্ভাবনা ভাষা ব্যবহার করার জন্য: পরীক্ষাটি সঠিক হওয়ার সম্ভাবনা 95%, তবে আপনি যা জানতে চান তা হ'ল আপনার এই রোগ হওয়ার সম্ভাবনা রয়েছে।

সামান্যভাবে বিষয়বস্তু: সমস্ত পাঠ্যপুস্তকগুলিতে সমাধানের জন্য বয়েস উপপাদ্য যে অন্যান্য ক্লাসিক উদাহরণটি মন্টি হল সমস্যা: আপনি একটি কুইজ শোতে এসেছেন। তিনটি দরজার একটির পিছনে একটি পুরষ্কার রয়েছে। আপনি একটি দরজা চয়ন করুন। কোনও পুরষ্কার প্রকাশের জন্য হোস্ট তিনটি দরজা খুলেছিল। সুযোগ পেয়ে কি আপনার দ্বার দ্বারে যেতে হবে?

আমি প্রশ্নের পুনর্নির্মাণ পছন্দ করি (নীচের রেফারেন্সের সৌজন্যে): আপনি কুইজ শোতে এসেছেন। এক মিলিয়ন দরজার পিছনে একটি পুরষ্কার রয়েছে। আপনি একটি দরজা চয়ন করুন। হোস্ট 104632 দরজা ব্যতীত অন্য কোনও দরজা খোলায় কোনও পুরষ্কার প্রকাশ না করে। আপনি 104632 দরজা পরিবর্তন করা উচিত?

আমার পছন্দের বই যা বায়েসের উপপাদ্যটি, বায়েসীয় দৃষ্টিকোণ থেকে অনেকটা আলোচিত, এটি ডেভিড জে সি ম্যাকের "ইনফরমেশন থিওরি, ইনফারেন্স অ্যান্ড লার্নিং অ্যালগরিদম"। এটি একটি কেমব্রিজ বিশ্ববিদ্যালয় প্রেস বই, আইএসবিএন -13: 9780521642989. আমার উত্তরটি (আমি আশা করি) বইটিতে যে ধরনের আলোচনার সৃষ্টি হয়েছে তার একটি বিশোধন। (সাধারণ নিয়ম প্রযোজ্য: লেখকের সাথে আমার কোনও সম্পর্ক নেই, আমি কেবল বইটি পছন্দ করি)।

3

বেইস উপপাদ্যটি এর সবচেয়ে সুস্পষ্ট আকারে কেবল দুটি জিনিসের পুনরায় বিবৃতি:

$P(HD|I)=P(DH|I)$
$P(HD|I)=P(H|I)P(D|HI)$

তাই প্রতিসাম্য ব্যবহার করে:

পি (এইচ ডি | আমি) = পি (এইচ | আমি) পি (ডি | এইচ আমি) = পি (ডি | আমি) পি (এইচ | ডি আমি)

$P(HD|I)=P(H|I)P(D|HI)=P(D|I)P(H|DI)$

$P(D|I) \neq 0$ $P(D|I)$

পি (এইচ | ডি আমি) = পি (এইচ | আমি) \frac{পি (ডি | এইচ আমি)}{পি (ডি | আমি)}

$P(H|DI)=P(H|I)\frac{P(D|HI)}{P(D|I)}$

তাহলে এটাই? এত সাধারণ কিছু এত ভয়ঙ্কর কীভাবে হতে পারে? বেশিরভাগ জিনিসের মতোই "এটি তার যাত্রা যা গন্তব্যের চেয়ে গুরুত্বপূর্ণ" " বায়েসের উপপাদ্য হ'ল যুক্তিগুলির কারণে যা এটির দিকে নিয়ে যায়।

$P(H|I)=1-P(\overline{H}|I)$

ডিডুকটিভ লজিকের এখন "নিয়ম" হ'ল যদি আপনার "A ইম্প্লি বি" এর সাথে সম্পর্ক থাকে তবে আপনার কাছে "নট বি ইম্প্লিও নট এ "ও রয়েছে। সুতরাং আমাদের কাছে "ধারাবাহিক যুক্তি বোঝায় বেয়েস উপপাদ্য"। এর অর্থ "নো বেয়েস উপপাদ্যটি সুসংগত যুক্তিযুক্ত নয়" means উদাহরণস্বরূপ, যদি আপনার ফলাফল কিছু পূর্ব এবং সম্ভাবনার জন্য কোনও বায়েশিয়ান ফলাফলের সমতুল্য না হয় তবে আপনি বেমানান যুক্তি দিয়ে যাচ্ছেন।

এই ফলাফলটিকে কক্সের উপপাদ্য বলা হয় এবং 1940 এর দশকে "সম্ভাব্য অনুক্রমের বীজগণিত" তে প্রমাণিত হয়েছিল। প্রবিলিটি তত্ত্বে আরও একটি সাম্প্রতিক ডেরিভেশন দেওয়া হয়েছে: বিজ্ঞানের যুক্তি।

— probabilityislogic
সূত্র

2

আমি সত্যিই কেভিন মরফির পরিচয় বেইস উপপাদ্য http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html তে পছন্দ করি

এখানে উদ্ধৃতিটি একটি অর্থনীতিবিদ নিবন্ধ থেকে:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

বয়েসিয়ান পদ্ধতির সারমর্মটি হ'ল একটি গাণিতিক নিয়ম প্রদান করা যা আপনাকে কীভাবে নতুন প্রমাণের আলোকে আপনার বিদ্যমান বিশ্বাসগুলি পরিবর্তন করতে হবে তা ব্যাখ্যা করে। অন্য কথায়, এটি বিজ্ঞানীদের তাদের বিদ্যমান জ্ঞান বা দক্ষতার সাথে নতুন ডেটা একত্রিত করার অনুমতি দেয়। ক্যানোনিকাল উদাহরণটি হ'ল কল্পনা করা যে কোনও প্রসূত নবজাতক তার প্রথম সূর্যাস্ত পর্যবেক্ষণ করে এবং সূর্যটি আবার উঠবে কি না, তা অবাক করে দেয়। তিনি উভয় সম্ভাব্য ফলাফলের জন্য সমান পূর্বের সম্ভাব্যতা নির্ধারণ করে এবং একটি সাদা এবং একটি কালো মার্বেল একটি ব্যাগে রেখে এটি উপস্থাপন করেন। পরের দিন, যখন সূর্য ওঠে তখন শিশুটি ব্যাগে একটি আরও সাদা মার্বেল রাখে। কোনও মার্বেল ব্যাগ থেকে এলোমেলোভাবে উত্থাপিত হওয়ার সম্ভাবনাটি সাদা হবে (অর্থাত্ ভবিষ্যতের সানরাইসিসে শিশুর বিশ্বাসের ডিগ্রি) এভাবে অর্ধেক থেকে দুই-তৃতীয়াংশ হয়ে গেছে। পরদিন সূর্যোদয়ের পরে, শিশুটি আরও একটি সাদা মার্বেল যুক্ত করে, এবং সম্ভাবনা (এবং এইভাবে বিশ্বাসের ডিগ্রি) দুই তৃতীয়াংশ থেকে তিন-চতুর্থাংশে যায়। ইত্যাদি। আস্তে আস্তে, প্রাথমিকভাবে বিশ্বাস করা যে সূর্য প্রতি সকালে ওঠার সম্ভাবনা নেই ঠিক ততটুকু পরিবর্তিত হয়ে এটি একটি দৃ certain়তা হয়ে উঠেছে যে সূর্য সবসময় উঠবে।

— kgarten
সূত্র